题目内容
多项式2x4-5x3+x2+5x-3中不可能含有的因式是( )
| A、x+1 | B、x-1 |
| C、x-2 | D、2x-3 |
考点:多项式
专题:
分析:将多项式进行因式分解,然后找出不可能含有的选项.
解答:解:2x4-5x3+x2+5x-3
=2x4+x2-3-5x3+5x
=(2x2+3)(x2-1)-5x(x2-1)
=(x2-1)(2x2-5x+3)
=(x+1)(x-1)(2x-3)(x-1),
多项式存在的因式为:x+1,x-1,2x-3,
不含有的因式为x-2.
故选C.
=2x4+x2-3-5x3+5x
=(2x2+3)(x2-1)-5x(x2-1)
=(x2-1)(2x2-5x+3)
=(x+1)(x-1)(2x-3)(x-1),
多项式存在的因式为:x+1,x-1,2x-3,
不含有的因式为x-2.
故选C.
点评:本题考查了多项式的知识,解答本题的关键是进行因式分解,找出所有的因式.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
多项式3x2y2-2x3y-1是( )
| A、二次三项式 |
| B、三次二项式 |
| C、四次三项式 |
| D、五次三项式 |
4的算术平方根为( )
| A、2 | B、±2 | C、-2 | D、16 |
 如图是由3块面积相同的瓷砖镶嵌而成的长方形地面示意图,一只小鸟随机落在阴影部分的概率为( )
如图是由3块面积相同的瓷砖镶嵌而成的长方形地面示意图,一只小鸟随机落在阴影部分的概率为( )A、
| ||
B、
| ||
C、
| ||
| D、1 |

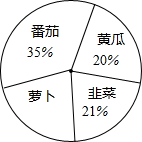 阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图.
阿姨在一块蔬菜地里种植了4种不同的蔬菜,各种蔬菜的种植面积分布如图. 如图,在△ABC中,∠C=90°,∠BAC=60°,AC=1,点D在BC上,点E在AB上,使得△ADE是等腰直角三角形,∠ADE=90°,求BE的长.(提示:可以运用“直角三角形中,30°角所对的直角边等于斜边的一半”).
如图,在△ABC中,∠C=90°,∠BAC=60°,AC=1,点D在BC上,点E在AB上,使得△ADE是等腰直角三角形,∠ADE=90°,求BE的长.(提示:可以运用“直角三角形中,30°角所对的直角边等于斜边的一半”). 如图:
如图: