题目内容
13.已知线段AB=12,点C是线段AB的黄金分割点,且AC>BC,则AC-BC=12$\sqrt{5}$-24,AC•BC=144$\sqrt{5}$-288.分析 根据黄金分割点的定义,知AC是较长线段,是整个线段的$\frac{\sqrt{5}-1}{2}$倍,BC是较短线段,较短的线段=原线段的$\frac{3-\sqrt{5}}{2}$倍.把AB=12代入计算即可.
解答 解:由黄金分割点的定义,AC=$\frac{\sqrt{5}-1}{2}$AB=6$\sqrt{5}$-6,
BC=$\frac{3-\sqrt{5}}{2}$AB=18-6$\sqrt{5}$,
AC-BC=12$\sqrt{5}$-24,
AC•BC=144$\sqrt{5}$-288
故答案为:12$\sqrt{5}$-24;144$\sqrt{5}$-288.
点评 本题考查了黄金分割的定义:线段上一点把线段分为较长线段和较短线段,若较长线段是较短线段和整个线段的比例中项,则这个点叫这条线段的黄金分割点.

练习册系列答案
相关题目
3.下列图形,属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
1.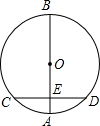 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
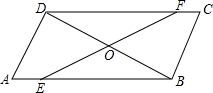 如图,?ABCD中,点E、F分别在AB、CD上,且AE=CF,EF与BD相交于点O,求证:OB=OD.
如图,?ABCD中,点E、F分别在AB、CD上,且AE=CF,EF与BD相交于点O,求证:OB=OD.