题目内容
19.已知PA、PB是⊙O的两条切线,点C是⊙O上异于A、B的一点,过C点的切线交PA、PB于D、E两点,若∠APB=40°,则∠DOE=70°或110°.分析 根据题意画出符合条件的两种图形,求出∠AOB的值,求出∠DOE=∠DOC+∠EOC=$\frac{1}{2}$∠AOC+$\frac{1}{2}$∠BOC,代入即可求出答案.
解答 解:分为两种情况:
①如图1,连接OA、OB、OC,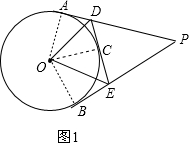
∵PA、PB是⊙O的切线,A、B为切点,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠APB=40°,
∴∠AOB=360°-90°-90°-40°=140°,
∵DE切⊙O于C,
∴OC⊥DE,
∴∠DCO=∠ECO=90°,
∵PA、PB、DE是⊙O的切线,切点是A、B、C,
∴∠ADO=∠CDO,∠CEO=∠BEO,
∵∠AOD=180°-∠OAD-∠ADO,∠COD=180°-∠OCD-∠CDO,
∴∠AOD=∠COD,
同理可证:∠COE=∠BOE,
∴∠DOE=∠DOC+∠EOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×140°=70°;
②如图2,∠DOE=$\frac{1}{2}$×(360°-140°)=110°.
故答案为:70°或110°.
点评 本题考查了切线的性质,切线长定理,三角形的内角和定理等知识点的应用,主要考查学生运用定理进行推理和计算的能力,题目比较好,有一定的难度,注意符合条件的有两种情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.将分式方程$\frac{2}{x-2}=\frac{1}{x}$去分母后得到正确的整式方程是( )
| A. | x-2=x | B. | x2-2x=2x | C. | x-2=2x | D. | x=2x-4 |
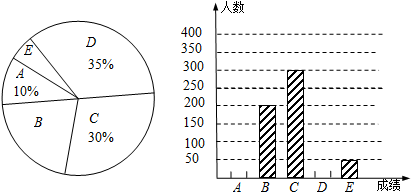
 如图,点A在直线l上,请在直线l上另找一点C,使△ABC是等腰三角形.请找出所有符合条件的点(保留作图痕迹).
如图,点A在直线l上,请在直线l上另找一点C,使△ABC是等腰三角形.请找出所有符合条件的点(保留作图痕迹).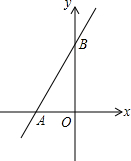 如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).
如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).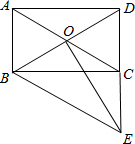 如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.
如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.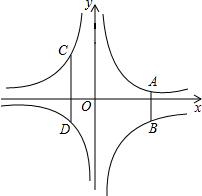 如图,已知点A,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥y轴,AB,CD在x轴的两侧,AB=1,CD=2,AB与CD的距离为3,则a-b的值是2.
如图,已知点A,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥y轴,AB,CD在x轴的两侧,AB=1,CD=2,AB与CD的距离为3,则a-b的值是2.