题目内容
12．选择合适的方法将下列一组分式化成同分母分式．$\frac{{a}^{2}-2ab}{{a}^{2}-4ab+4{b}^{2}}$，$\frac{b-a}{2b-a}$，$\frac{a+2b}{{a}^{2}-4{b}^{2}}$．
分析 首先将分式分解因式进而化简求出答案．
解答 解：$\frac{{a}^{2}-2ab}{{a}^{2}-4ab+4{b}^{2}}$=$\frac{a（a-2b）}{（a-2b）^{2}}$=$\frac{a}{a-2b}$，
$\frac{b-a}{2b-a}$=$\frac{a-b}{a-2b}$，
$\frac{a+2b}{{a}^{2}-4{b}^{2}}$=$\frac{a+2b}{（a-2b）（a+2b）}$=$\frac{1}{a-2b}$．
点评 此题主要考查了通分，正确因式分解是解题关键．
练习册系列答案
相关题目
3．下列调查中，最适合采用抽样调查的是（ ）
| A． | 对旅客上飞机前的安检 | |
| B． | 了解全班同学每周体育锻炼的时间 | |
| C． | 调查奥运会金牌获得者的兴奋剂使用情况 | |
| D． | 调查我国居民对汽车废气污染环境的看法 |
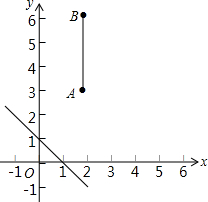如果，在平面直角坐标系中，已知点A（2，3）、B（2，6），连接AB，如果点P在直线y=-x+1上，且点P到直线的距离小于1，那么点P是线段AB的“环绕点”，若点Q（m，n）是线段AB的“环绕点”，求n的取值范围．
7．将分式方程$\frac{2}{x-2}=\frac{1}{x}$去分母后得到正确的整式方程是（ ）
| A． | x-2=x | B． | x2-2x=2x | C． | x-2=2x | D． | x=2x-4 |
-$\frac{{x}^{2}-1}{{x}^{2}-2x+1}$）÷$\frac{x}{x+1}$=$\frac{x+1}{x-1}$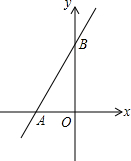
如图，平面直角坐标系中，点O为坐标原点，一次函数的图象过点（-1，4）与点（3，12）．
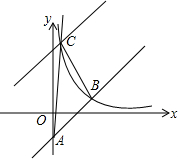如图，已知直线y=x+a与y轴相交于点A，与反比例函数y=$\frac{k}{x}$（x＞0）的图象相交于点B（-a+1，a+4）．