题目内容
3. 如图:∠AOB=45°,P是∠AOB内一点,PO=10,C、D分别是OA、OB上的动点,求△PCD周长最小值.
如图:∠AOB=45°,P是∠AOB内一点,PO=10,C、D分别是OA、OB上的动点,求△PCD周长最小值.
分析 设点P关于OA、OB对称点分别为M、N,当点C、D在MN上时,△PCD周长为PC+CD+DP=MN,此时周长最小.
解答  解:分别作点P关于OA、OB的对称点M、N,连接OM、ON、MN,MN交OA、OB于点C、D,连接PC、PD,此时△PCD周长的最小值等于MN.
解:分别作点P关于OA、OB的对称点M、N,连接OM、ON、MN,MN交OA、OB于点C、D,连接PC、PD,此时△PCD周长的最小值等于MN.
由轴对称性质可得OM=ON=OP=10,∠MOA=∠POA,∠NOB=∠POB,
则∠MON=2∠AOB=2×45°=90°,
在Rt△MON中,MN=$\sqrt{O{M}^{2}+O{N}^{2}}$=10$\sqrt{2}$.
即△PCD周长的最小值等于10$\sqrt{2}$.
点评 本题考查了轴对称--最短路线的问题,综合应用了轴对称、等腰直角三角形以及勾股定理的有关知识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.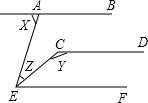 如图,AB∥CD∥EF,则下列各式中等于180°的是( )
如图,AB∥CD∥EF,则下列各式中等于180°的是( )
 如图,AB∥CD∥EF,则下列各式中等于180°的是( )
如图,AB∥CD∥EF,则下列各式中等于180°的是( )| A. | ∠X+∠Y+∠Z | B. | ∠Y+∠Z-∠X | C. | ∠X-∠Y+∠Z | D. | ∠X+∠Y-∠Z |
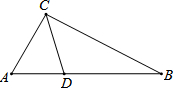 交通对城市的发展发挥着十分重要的作用,如图,B市位于A市的正东方向,原来从A市到B市要经过C市,C市位于A市北偏东30°方向,位于B市北偏西53°方向,A到C的距离为150千米,现从A、B之间新修了一条直达的高速公路AB.
交通对城市的发展发挥着十分重要的作用,如图,B市位于A市的正东方向,原来从A市到B市要经过C市,C市位于A市北偏东30°方向,位于B市北偏西53°方向,A到C的距离为150千米,现从A、B之间新修了一条直达的高速公路AB. 如图,?BDEF的顶点D,E,F分别在△ABC三边AB,AC,BC上,求证:△ADE∽△EFC.
如图,?BDEF的顶点D,E,F分别在△ABC三边AB,AC,BC上,求证:△ADE∽△EFC.