题目内容
13.在平面直角坐标系中,己知A(0,1),B(4,3),点M在坐标轴上,使∠AMB=45°,则M的坐标为(0,7),(0,-1),(3-$\sqrt{10}$,0),(3+$\sqrt{10}$,0).分析 根据圆周角定理,如果$\widehat{AB}$所对圆心角的度数为90°,且M与点A,B共圆,则∠AMB=45°.由此假设△PAB是以点P为直角顶点的等腰直角三角形(P在AB上方),那么PA=PB=$\frac{\sqrt{2}}{2}$AB=$\sqrt{10}$,再求出P(1,4),以P为圆心,PA为半径画圆交y轴于M,则∠AMB=$\frac{1}{2}$∠APB=45°,此时PM=$\sqrt{10}$,PE=1,ME=$\sqrt{(\sqrt{10})^{2}-1}$=3,则M1(0,7);在AB下方再求出另一个圆心P′(3,0),以P′为圆心,P′A为半径画圆交y轴于M2,交x轴于M3,M4,根据半径为$\sqrt{10}$,即可求出M2(0,-1),M3(3-$\sqrt{10}$,0),M4(3+$\sqrt{10}$,0).
解答 解:∵A(0,1),B(4,3),
∴AB=$\sqrt{{4}^{2}+(3-1)^{2}}$=2$\sqrt{5}$.
如图,如果△PAB是以点P为直角顶点的等腰直角三角形(P在AB上方),那么PA=PB=$\frac{\sqrt{2}}{2}$AB=$\sqrt{10}$.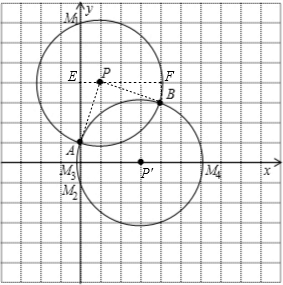
过P作PE⊥y轴于E,过B作BF⊥PE于F,易证△AEP≌△PFB,AE=PF,EP=BF.
设EP=a,AE=b,则EF=EP+PF=a+b=4,b+1=a+3,所以b=a+2,
解得a=1,b=3,则P(1,4).
以P为圆心,PA为半径画圆交y轴于M,则∠AMB=$\frac{1}{2}$∠APB=45°,此时PM=$\sqrt{10}$,PE=1,
ME=$\sqrt{(\sqrt{10})^{2}-1}$=3,则M1(0,7);
易求另一个圆心P′(3,0),以P′为圆心,P′A为半径画圆交y轴于M2,交x轴于M3,M4,
设M2(0,n),M3(m,0),
∵P′M2=$\sqrt{10}$,
∴32+n2=10,
解得n=±1(正数舍去),
∴M2(0,-1);
∵P′M3=$\sqrt{10}$,
∴|m-3|=$\sqrt{10}$,
解得m=3±$\sqrt{10}$,
∴M3(3-$\sqrt{10}$,0),M4(3+$\sqrt{10}$,0).
综上所述,所求点的坐标为M1(0,7),M2(0,-1),M3(3-$\sqrt{10}$,0),M4(3+$\sqrt{10}$,0).
故答案为(0,7),(0,-1),(3-$\sqrt{10}$,0),(3+$\sqrt{10}$,0).
点评 本题考查了坐标与图形的性质,圆周角定理,等腰直角三角形的性质,全等三角形的判定与性质,勾股定理等知识,有一定难度.利用数形结合、分类讨论是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | -l | C. | 1 或-1 | D. | 2 |
| A. | 抛掷一枚硬币,硬币落地时正面朝上是随机事件 | |
| B. | 把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 | |
| C. | 一个盒子中有白球m个,红球6个,黑球n个(每个球除了颜色外都相同),如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m+n=6 | |
| D. | 任意打开七年级下册数学教科书,正好是97页是确定事件 |
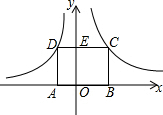 如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.
如图,矩形ABCD的顶点A在x轴负半轴上,点B在x轴正半轴,点C在反比例函数y=$\frac{4}{x}$第一象限的图象上,点D在反比例函数y=$\frac{k}{x}$的图象上,CD交y轴于点E.若DE:CE=1:2,则k的值是-2.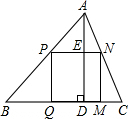 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S.
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成正方形零件PQMN,使正方形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.求这个正方形零件PQMN面积S. 如图:∠AOB=45°,P是∠AOB内一点,PO=10,C、D分别是OA、OB上的动点,求△PCD周长最小值.
如图:∠AOB=45°,P是∠AOB内一点,PO=10,C、D分别是OA、OB上的动点,求△PCD周长最小值.