题目内容
2.解方程组.(1)$\left\{\begin{array}{l}{2x-3y=-3,①}\\{3x+2y=3,②}\end{array}\right.$
(2)$\left\{\begin{array}{l}{5x-y=36,①}\\{3(x+y)-2(x-y)=28,②}\end{array}\right.$.
分析 (1)根据加减法,可得方程的解;
(2)根据代入法,可得方程的解.
解答 解:(1)①×2+②×3,得
13x=3,解得x=$\frac{3}{13}$,
将x=$\frac{3}{13}$代入①,得
y=$\frac{11}{13}$,
方程组的解是$\left\{\begin{array}{l}{x=\frac{3}{13}}\\{y=\frac{11}{13}}\end{array}\right.$;
(2)由①,得
y=5x-36③,
把③代入②,得
3(x+5x-36)-2(x-5x+36)=28,
解得x=$\frac{104}{13}$,
把x=$\frac{104}{13}$代入③,得
y=5×$\frac{104}{13}$-36=4,
方程组的解是$\left\{\begin{array}{l}{x=\frac{104}{13}}\\{y=4}\end{array}\right.$.
点评 本题考查了解二元一次方程组,加减消元法、代入消元法是解方程组的关键.

练习册系列答案
相关题目
13.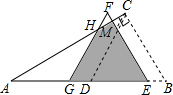 如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.
如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.
 如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.
如图,△ABC中,∠ACB=90°,∠CAB=30°,AB=4cm,D是AB的中点,现将△BCD沿BA方向平移1cm,得到△EFG,FG交AC于H,FE交AC于M,则△EFG与△ABC重叠部分的面积为( )cm2.| A. | $\frac{7\sqrt{3}}{8}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
17.一组数据1,0,-1,2,3的中位数是( )
| A. | 1 | B. | 0 | C. | -1 | D. | 2 |
11.不等式组$\left\{\begin{array}{l}{2x+1≤3}\\{x>-3}\end{array}\right.$中的两个不等式的解集在同一个数轴上表示正确的是( )
| A. | 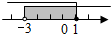 | B. | 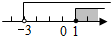 | C. | 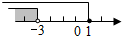 | D. | 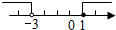 |
8.景新中学为了了解学生体育中考备考情况,随机抽查了10名学生的引体向上,结果如下表:
则关于这10名学生的引体向上数据,下列说法错误的是( )
| 引体向上(次) | 18 | 19 | 20 |
| 学生数 | 2 | 6 | 2 |
| A. | 极差是2 | B. | 众数是19 | C. | 平均数是19 | D. | 方差是4 |
9.下列各式运算结果为a5的是( )
| A. | (a2)3 | B. | a2+a3 | C. | a2•a3 | D. | a10÷a2 |
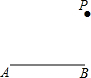 如图所示,已知:线段AB和点P.请用尺规按下列要求作图:①延长AB到C,使BC=2AB;②作射线BP;③连接PA,PC.
如图所示,已知:线段AB和点P.请用尺规按下列要求作图:①延长AB到C,使BC=2AB;②作射线BP;③连接PA,PC.