题目内容
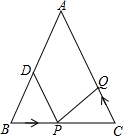
11.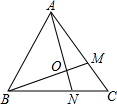 在等边△ABC中,M是AC上一点,N是BC上的一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )
在等边△ABC中,M是AC上一点,N是BC上的一点,且AM=BN,∠MBC=25°,AN与BM交于点O,则∠MON的度数为( )| A. | 110° | B. | 105° | C. | 90° | D. | 85° |
分析 根据等边三角形的性质可得∠A=∠B=60°,又因为AM=BN,AB=AB,所以△AMB≌△BNA,从而得到∠NAB=∠MBA=60°-∠MBC=35°,则∠MON=∠AOB=180°-2×35°=110°.
解答 解:∵△ABC是等边三角形,
∴∠A=∠B=60°,
∵AM=BN,AB=AB,
在△AMB与△BNA中,
$\left\{\begin{array}{l}{AM=BN}\\{∠A=∠B=60°}\\{AB=AB}\end{array}\right.$,
∴△AMB≌△BNA(SAS),
∴∠NAB=∠MBA=60°-∠MBC=35°,
∴∠AOB=180°-2×35°=110°,
∵∠MON=∠AOB,
∴∠MON=110°.
故选A.
点评 此题考查全等三角形的判定和性质,根据等边三角形的性质,结合全等三角形求解.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
2.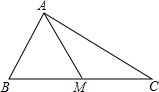 如图,AM是△ABC的中线,若△ABM的面积为4,则△ABC的面积为( )
如图,AM是△ABC的中线,若△ABM的面积为4,则△ABC的面积为( )
 如图,AM是△ABC的中线,若△ABM的面积为4,则△ABC的面积为( )
如图,AM是△ABC的中线,若△ABM的面积为4,则△ABC的面积为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
6.如果|a+2|+(b-1)2=0,则(a+b)2008的值是( )
| A. | -2008 | B. | 2008 | C. | -1 | D. | 1 |
20.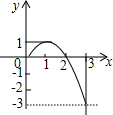 已知二次函数y=ax2+bx+c(a≠0)(0≤x≤3)的图象如图所示,则该函数在所给自变量取值范围内,下列说法正确的是( )
已知二次函数y=ax2+bx+c(a≠0)(0≤x≤3)的图象如图所示,则该函数在所给自变量取值范围内,下列说法正确的是( )
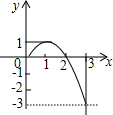 已知二次函数y=ax2+bx+c(a≠0)(0≤x≤3)的图象如图所示,则该函数在所给自变量取值范围内,下列说法正确的是( )
已知二次函数y=ax2+bx+c(a≠0)(0≤x≤3)的图象如图所示,则该函数在所给自变量取值范围内,下列说法正确的是( )| A. | 有最大值1,没有最小值 | B. | 有最大值3,有最小值-3 | ||
| C. | 有最大值1,有最小值-3 | D. | 有最大值3,有最小值1 |
 如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.
如图所示,已知△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.