题目内容
6．
如图，一轮船以16海里/时的速度从港口A出发向东北方向航行，另一轮船以12海里/时的速度同时从港口A出发向东南方向航行，离开港口2小时后，则两船相距（ ）| A． | 25海里 | B． | 30海里 | C． | 40海里 | D． | 50海里 |
分析 首先根据路程=速度×时间可得AC、AB的长，然后连接BC，再利用勾股定理计算出BC长即可．
解答 
解：连接BC，
由题意得：AC=16×2=32（海里），AB=12×2=24（海里），
CB=$\sqrt{A{C}^{2}+A{B}^{2}}$=40（海里），
故选：C．
点评 此题主要考查了勾股定理的应用，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图，学校在小明家北偏西45度的方向上，距离约是500米．
17．小华和小刚兄弟两个同时从家去同一所学校上学，速度都是每分钟走50米．小华从家到学校走直线用了10分钟，而小刚从家出发先去找小明再到学校（均走直线），小刚到小明家用了6分钟，小明家到学校用了8分钟，小刚上学走了个（ ）
| A． | 锐角弯 | B． | 钝角弯 | C． | 直角弯 | D． | 不能确定 |
14．下列四个点，在正比例函数y=-$\frac{5}{2}$x的图象上的点是（ ）
| A． | （2，5） | B． | （5，2） | C． | （2，-5） | D． | （5，-2） |
1．能判定△ABC∽△A′B′C′的条件是（ ）
| A． | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$，∠B=∠B′ | B． | $\frac{AB}{A′C′}$=$\frac{A′B′}{AC}$，∠B=∠B′ | ||
| C． | $\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$，∠A=∠A′ | D． | $\frac{AB}{A′B′}$=$\frac{AC}{B′C′}$，∠A=∠A′ |
18．
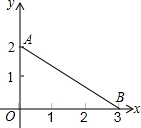如图，线段AB对应的函数表达式为（ ）
如图，线段AB对应的函数表达式为（ ）| A． | y=-$\frac{3}{2}$x+2 | B． | y=-$\frac{2}{3}$x+2 | C． | y=-$\frac{2}{3}$x+2（0≤x≤3） | D． | y=-$\frac{2}{3}$x+20（0＜x＜3） |
建立直角坐标系，描出下列各点A（-2，2），B（-1，0），C（0，2）