题目内容
14.下列四个点,在正比例函数y=-$\frac{5}{2}$x的图象上的点是( )| A. | (2,5) | B. | (5,2) | C. | (2,-5) | D. | (5,-2) |
分析 先计算出自变量为2和5时的函数值,然后根据一次函数图象上点的坐标特征进行判断.
解答 解:当x=2时,y=-$\frac{5}{2}$x=-5;当x=5时,y=-$\frac{5}{2}$x=-$\frac{25}{2}$,
所以点(2,-5)在正比例函数y=-$\frac{5}{2}$x的图象上.
故选C.
点评 本题考查了一次函数图象上点的坐标特征:直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
相关题目
4.下列运算正确的是( )
| A. | 2+$\sqrt{3}$=2$\sqrt{3}$ | B. | 5$\sqrt{2}$-$\sqrt{2}$=5 | C. | 5$\sqrt{2a}$+$\sqrt{2a}$=6$\sqrt{2a}$ | D. | $\sqrt{y}$+2$\sqrt{x}$=3$\sqrt{xy}$ |
6. 如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
 如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )
如图,一轮船以16海里/时的速度从港口A出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后,则两船相距( )| A. | 25海里 | B. | 30海里 | C. | 40海里 | D. | 50海里 |
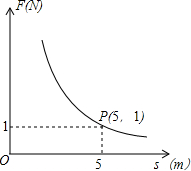 在对物体做功一定情况下,力F(N)与物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,则当力达到10N时,物体在力的方向上移动的距离是0.5m.
在对物体做功一定情况下,力F(N)与物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,则当力达到10N时,物体在力的方向上移动的距离是0.5m. 将图中△ABC,以点G为位似中心,缩小为原来的0.5倍,得到△A′B′C′,写出变化前后两个三角形各顶点的坐标.
将图中△ABC,以点G为位似中心,缩小为原来的0.5倍,得到△A′B′C′,写出变化前后两个三角形各顶点的坐标. 某博物馆通过浮动门票价格的方法既保证必要的收入,又要尽量控制参观人数,调查统计发现,每周参观人数与票价之间的关系可近似的看成如图所示的一次函数关系.如果门票价格定为6元,那么本周大约有9000人参观.
某博物馆通过浮动门票价格的方法既保证必要的收入,又要尽量控制参观人数,调查统计发现,每周参观人数与票价之间的关系可近似的看成如图所示的一次函数关系.如果门票价格定为6元,那么本周大约有9000人参观.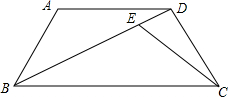 如图.梯形ABCD中.AD∥BC,AB=CD=2,AD=4,BC=6,点E在BD上,且∠DCE=∠ADB.
如图.梯形ABCD中.AD∥BC,AB=CD=2,AD=4,BC=6,点E在BD上,且∠DCE=∠ADB.