题目内容
1．观察算式：1=12；1+3=4=22；1+3+5=9=32；1+3+5+7=16=42；1+3+5+7+9=25=52，…，根据以上规律：1+3+5+7+…+99=502．分析 观察算式可知：1个奇数1等于12，从1开始两个连续奇数的和等于22，三个连续奇数的和等于32，四个连续奇数的和等于42，五个连续奇数的和等于52，…，由此得出n个连续奇数的和是n2，由此求得答案即可．
解答 解：∵1=12；
1+3=4=22；
1+3+5=9=32；
1+3+5+7=16=42；
1+3+5+7+9=25=52，
…，
∴1+3+5+…+99=502．
故答案为：502．
点评 此题考查数字的变化规律，找出从1开始n个连续奇数的和是n2，得出规律解决问题．
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，∠C=∠ABC，AE∥BC，BE平分∠ABC，则下列结论中一定成立的是①②④（把所有正确结论的序号都填在横线上）．
如图，已知∠AOB=60°，点P是OA边上，OP=8cm，点M、N在边OB上，PM=PN，若MN=2cm，则ON=5cm．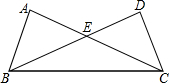
如图，在Rt△ABC和Rt△BCD中，∠A=∠D=90°，AB=CD=4，BC=$4\sqrt{5}$，△BCE的面积=10．