Question

13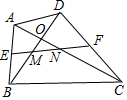．如图．在四边形ABCD中．AC=BD，E，F分别为AB，CD的中点（O，M，N不重合），仔细观察你会发观．无论四边形ABCD的形状如何变化，只要保待对角线相等，则EF与两条对角线围成的三角形总是等腰三角形（图中的△OMN），请说明理由．

Answer 1

分析 取AD的中点Q，连接EQ、FQ，根据三角形的中位线定理得出EQ∥AC，EQ=$\frac{1}{2}$BD，FQ=$\frac{1}{2}$AC，FQ∥AC，根据平行线得出∠QEF=∠OMN，∠QFE=∠ONM，求出QE=QF，推出∠QEF=∠QFE，求出∠OMN=∠ONM即可．

解答 解：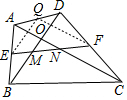
取AD的中点Q，连接EQ、FQ，
∵E，F分别为AB，CD的中点，
∴EQ∥AC，EQ=$\frac{1}{2}$BD，FQ=$\frac{1}{2}$AC，FQ∥AC，
∴∠QEF=∠OMN，∠QFE=∠ONM，
∵AC=BD，
∴QE=QF，
∴∠QEF=∠QFE，
∴∠OMN=∠ONM，
∴OM=ON，
即△OMN是等腰三角形．

点评 本题考查了等腰三角形的性质，三角形的中位线定理等知识点，能熟练地运用定理进行推理是解此题的关键．