题目内容
18．
如图，△ABC中，点D是AB边上的中点，DE∥BC交AC于点E（1）求证：点E是AC边的中点；
（2）连接BE、CD交于点O，求证：OC=2OD．
分析 （1）根据点D是AB边上的中点，DE∥BC可得出△ADE∽△ABC，进而可得出结论；
（2）根据题意可得出△ODE∽△OCB，据此可得出结论．
解答 （1）证明：∵DE∥BC，
∴△ADE∽△ABC．
∵D是AB边上的中点，
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$=$\frac{1}{2}$，
即点E是AC边的中点；
（2）证明：∵由（1）知，点E是AC边的中点，
∴DE是△ABC的中位线，
∴DE=$\frac{1}{2}$BC．
∵DE∥BC，
∴∠DEO=∠OBC，∠EDO=∠BCO，
∴△OED∽△OBC，
∴$\frac{OD}{OC}$=$\frac{DE}{BC}$=$\frac{1}{2}$，
∴OC=2OD．
点评 本题考查的是三角形中位线定理，熟知三角形的中位线平行于第三边，并且等于第三边的一半是解答此题的关键．
练习册系列答案
相关题目
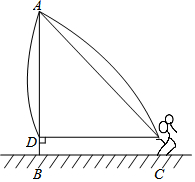想测量旗杆高度，一个绳子拴在旗杆的顶端自然垂落多了1米，一个小孩把绳子水平拉开5米使绳子被拉直，此时绳子底部距地面1米，问：旗杆多高？
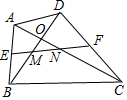如图．在四边形ABCD中．AC=BD，E，F分别为AB，CD的中点（O，M，N不重合），仔细观察你会发观．无论四边形ABCD的形状如何变化，只要保待对角线相等，则EF与两条对角线围成的三角形总是等腰三角形（图中的△OMN），请说明理由．
如图，在梯形ABCD中，AD∥BC，M、N分别为AB、DC的中点，对角线AC、BD分别交MN于E、F，求证：EF=$\frac{1}{2}$（BC-AD）．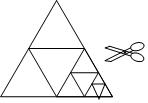
在一次数学综合实践课上，某同学将一张等边三角形纸片沿中位线剪成4个小三角形．称为第一次操作；然后，将其中的一个三角形按同样方式再剪成4个小三角形，共得到7个小三角形，称为第二次操作；再将其中一个三角形按同样方式再剪成4个小三角形，共得到10个小三角形，称为第三次操作；…根据以上操作，若要得到100个小三角形，则需要操作的次数是（ ）