题目内容
20．先化简，再求值：（x-1-$\frac{3}{x+1}$）÷$\frac{{x}^{2}-4x+4}{x+1}$，其中x=-4．分析 根据分式的减法和除法可以化简题目中的式子，然后将x的值代入化简后的式子即可解答本题．
解答 解：（x-1-$\frac{3}{x+1}$）÷$\frac{{x}^{2}-4x+4}{x+1}$
=$\frac{（x-1）（x+1）-3}{x+1}•\frac{x+1}{（x-2）^{2}}$
=$\frac{{x}^{2}-1-3}{x+1}•\frac{x+1}{（x-2）^{2}}$
=$\frac{（x+2）（x-2）}{x+1}•\frac{x+1}{（x-2）^{2}}$
=$\frac{x+2}{x-2}$，
当x=-4时，原式=$\frac{-4+2}{-4-2}=\frac{-2}{-6}=\frac{1}{3}$．
点评 本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
练习册系列答案
天天向上口算本系列答案
相关题目
如图，在△ABC中，∠A=60°，点D是BC边的中点，DE⊥BC，∠ABC的角平分线BF交DE于△ABC内一点P，连接PC．
15．我市某宾馆拥有客房100间，经营中发现：每天入住的客房数y（间）与房价x（元）（180≤x≤300）满足一次函数关系，部分对应值如表：
（1）求y与x之间的函数表达式；
（2）已知每间入住的客房，宾馆每日需支出各种费用80元；每日空置的客房，宾馆每日需支出40元，当房价为多少元时，宾馆当日利润最大？求出最大值．（宾馆当日利润=当日房费收入-当日支出）
| x（元） | 180 | 210 | 260 | 300 |
| y（间） | 100 | 85 | 60 | 40 |
（2）已知每间入住的客房，宾馆每日需支出各种费用80元；每日空置的客房，宾馆每日需支出40元，当房价为多少元时，宾馆当日利润最大？求出最大值．（宾馆当日利润=当日房费收入-当日支出）
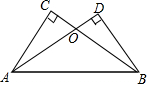如图，AD、BC相交于点O，AD=BC，∠C=∠D=90°．
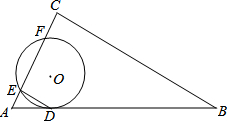如图，⊙O与Rt△ABC的斜边AB相切于点D，与直角边AC相交于E、F两点，连结DE，已知∠B=30°，⊙O的半径为6，弧DE的长度为2π．