题目内容
20.在Rt△ABC中,∠ACB=90°,CD⊥AB于D,则BD:AD等于( )| A. | a:b | B. | a2:b2 | C. | $\sqrt{a}$:$\sqrt{b}$ | D. | 不能确定 |
分析 由在△ABC中,∠ACB=90°,CD⊥AB,即可证得∠ADC=∠BDC=90°,又由同角的余角相等,证得∠A=∠BCD,根据有两角对应相等的三角形相似,证得△ACD∽△CBD∽△ABC,然后由相似三角形的对应边成比例,证得结论.
解答 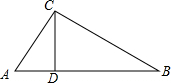 证明:在△ABC中,AB=c,AC=b,BC=a,
证明:在△ABC中,AB=c,AC=b,BC=a,
∵∠ACB=90°,CD⊥AB,
∴∠ADC=∠BDC=90°,∠ACD+∠BCD=90°,
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD∽△ABC,
∴$\frac{AC}{AD}=\frac{AB}{AC}$,$\frac{BC}{AB}=\frac{BD}{BC}$,
即:b2=c•AD,a2=c•BD,
∴BD:AD=a2:b2,
故选B.
点评 此题考查了相似三角形的判定与性质以及直角三角形的性质.此题难度适中,注意有两角对应相等的三角形相似定理的应用,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
10.关于方程y2+y+1=0的说法正确的是( )
| A. | 两实数根之和为-1 | B. | 两实数根之积为1 | ||
| C. | 两实数根之和为1 | D. | 无实数根 |
9.已知x2+2mx+16是完全平方式,则m的值是( )
| A. | ±4 | B. | 4 | C. | -4 | D. | ±8 |