题目内容
4. 如图所示,已知抛物线y=ax2-4x-5(a>0,a为常数)与一次函数y=$\frac{1}{2}$x+b(b为常数)交于点M(6,n),直线y=$\frac{1}{2}$x+b与x轴及y轴交于两点A、B,△AOB的周长是12+4$\sqrt{5}$,抛物线y=ax2-4x-5与y轴交于点C,与x轴交于点D、E(点E在点D的右侧).
如图所示,已知抛物线y=ax2-4x-5(a>0,a为常数)与一次函数y=$\frac{1}{2}$x+b(b为常数)交于点M(6,n),直线y=$\frac{1}{2}$x+b与x轴及y轴交于两点A、B,△AOB的周长是12+4$\sqrt{5}$,抛物线y=ax2-4x-5与y轴交于点C,与x轴交于点D、E(点E在点D的右侧).(1)确定a、b、n及tan∠BAO的值;
(2)确定一次函数y=$\frac{1}{2}$x+b与抛物线y=ax2-4x-5的另一个交点N的坐标,并计算线段MN的长度;
(3)试确定在抛物线及对称轴上是否存在两点P、Q,使得四边形C、E、Q、P是平行四边形?如果存在请直接写出P、Q两点坐标;如果不存在,请说明理由.
分析 (1)用b表示A、B坐标,根据△AOB周长求出b,再求出点M坐标,即可解决问题.
(2)列方程组解方程组即可解决问题.
(3)分CE为对角线,CE为边两种情形讨论即可.
解答 解:(1)∵直线y=$\frac{1}{2}$x+b与x轴及y轴交于两点A、B,
∴点A坐标(-2b,0),点B坐标(0,b),
∴OB=b,OA=2b,AB=$\sqrt{5}$b,
∵△AOB的周长为12+4$\sqrt{5}$,
∴3b+$\sqrt{5}$b=12+4$\sqrt{5}$,
∴b=4,
∴直线解析式为y=$\frac{1}{2}$x+4,把点M(6,n)代入得到n=7,
∴点M坐标(6,7),代入抛物线解析式得到:7=36a-24-5,
∴a=1,
∴OB=4,OA=8,
∴tanBAO=$\frac{OB}{OA}$=$\frac{1}{2}$.
∴a=1,b=4,n=7,tan∠BAO=$\frac{1}{2}$,
(2)由$\left\{\begin{array}{l}{y=\frac{1}{2}x+4}\\{y={x}^{2}-4x-5}\end{array}\right.$解得$\left\{\begin{array}{l}{x=6}\\{y=7}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=\frac{13}{4}}\end{array}\right.$,
∴一次函数y=$\frac{1}{2}$x+b与抛物线y=ax2-4x-5的另一个交点N的坐标(-$\frac{3}{2}$,$\frac{13}{4}$).
∴MN=$\sqrt{(-\frac{3}{2}-6)^{2}+(\frac{13}{4}-7)^{2}}$=$\frac{15\sqrt{5}}{4}$.
(3)如图,点C(0,-5),点E(5,0),抛物线顶点(2,-9),
①当CE为对角线时,点P1与顶点重合时,四边形CP1EQ1是平行四边形,
∵P1(2,-9),CE与对称轴的交点坐标G(2,-2.5),
∴GP1=GQ1=6.5,
∴Q1(2,4).
②当CE为边时,∵CE=P2Q2,
∴|xQ-xP|=|xE-xC|=5,|yE-yC|=|yQ-yP|=5,
∴P2、P3的横坐标分别为-3,7,
∵x=-3时,y=12,x=7时,y=16,
∴P2(-3,16),Q2(2,17),P3(7,16),Q3(2,12).
综上所述P1(2,-9),Q1(2,4),P2(-3,16),Q2(2,17),P3(7,16),Q3(2,12).
点评 本题考查二次函数综合题、两点间距离公式、平行四边形等知识,解题的关键是灵活掌握待定系数法,学会利用方程组求两个函数的图象的交点坐标,学会分类讨论,属于中考压轴题.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | a=3,b=1 | B. | a=-3,b=1 | C. | a=3,b=-1 | D. | a=-3,b=-1 |
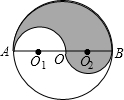 如图,⊙O的半径为1,分别以⊙O的直径AB上的两个四等分点O1,O2为圆心,$\frac{1}{2}$为半径作圆,则图中阴影部分的面积为( )
如图,⊙O的半径为1,分别以⊙O的直径AB上的两个四等分点O1,O2为圆心,$\frac{1}{2}$为半径作圆,则图中阴影部分的面积为( )| A. | π | B. | $\frac{1}{2}$π | C. | $\frac{1}{4}$π | D. | 2π |
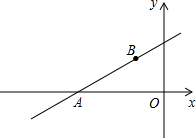 如图,直线l:y=$\frac{{\sqrt{3}}}{3}$x+m与x轴交于A点,且经过点B(-$\sqrt{3}$,2).已知抛物线C:y=ax2+bx+9与x轴只有一个公共点,恰为A点.
如图,直线l:y=$\frac{{\sqrt{3}}}{3}$x+m与x轴交于A点,且经过点B(-$\sqrt{3}$,2).已知抛物线C:y=ax2+bx+9与x轴只有一个公共点,恰为A点.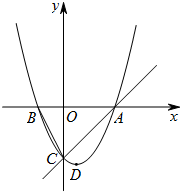 如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.