题目内容
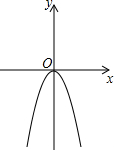
12.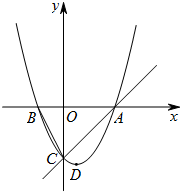 如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
如图,已知抛物线y=ax2+bx+c的顶点D的坐标为(1,-$\frac{9}{2}$),且与x轴交于A,B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.(1)求抛物线所对应的二次函数的表达式.
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围.
(3)是否存在P点,使∠PAC=∠BCO?若存在,请直接写出点P的坐标;若不存在,请说明理由.
分析 (1)设抛物线为y=a(x-1)2-$\frac{9}{2}$,把点(4,0)代入即可解决问题.
(2)如图1中,求出∠PAO=45°时点P的坐标,由此即可解决问题.
(3)存在.如图2中,∠P1AO=∠BCO,设AP1交y轴于E,理由相似三角形求出OE的长,再求出直线CE与抛物线的交点即可解决问题,根据对称性再求出P2坐标即可.
解答 解:(1)设抛物线为y=a(x-1)2-$\frac{9}{2}$,
∵抛物线经过点(4,0),
∴0=9a-$\frac{9}{2}$,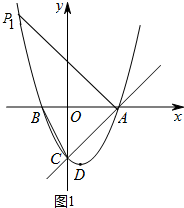
∴a=$\frac{1}{2}$,
∴抛物线为y=$\frac{1}{2}$(x-1)2-$\frac{9}{2}$.
(2)∵y=$\frac{1}{2}$(x-1)2-$\frac{9}{2}$.
令x=0,则y=-4,∴点C坐标(0,-4),
令y=0,(x-1)2=9,解得x=-2或4,
∴点B坐标(-2,0),点A坐标(4,0).
∴OA=OC,
∴∠OAC=∠OCA=45°,
如图1中,过点A作直线AP1⊥AC,交抛物线于P1,
∵直线AC为y=x-4,
∴直线AP1为y=-x+4,
由$\left\{\begin{array}{l}{y=-x+4}\\{y=\frac{1}{2}(x-1)^{2}-\frac{9}{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-4}\\{y=8}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$,
∴点P1坐标(-4,8),
∴当点P在P1与C之间时,∠PAO不大于45°,
∴-4≤m≤0.
(3)存在.
理由:如图2中,设PA交y轴于M,作MN⊥AC于N.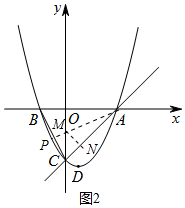
设MN=CN=x,
∵∠MAN=∠BCO,
∴tan∠MAN=tan∠BCO=$\frac{1}{2}$,
∴AN=2x,
∴AC=CN+AN=4$\sqrt{2}$,
∴3x=4$\sqrt{2}$,
∴x=$\frac{4\sqrt{2}}{3}$,
∴MC=$\sqrt{2}$x=$\frac{8}{3}$,OM=4-$\frac{8}{3}$=$\frac{4}{3}$.
∴M(0,-$\frac{4}{3}$),
∴直线PA的解析式为y=$\frac{1}{3}$x-$\frac{4}{3}$,
由$\left\{\begin{array}{l}{y=\frac{1}{3}x-\frac{4}{3}}\\{y=\frac{1}{2}{x}^{2}-x-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{4}{3}}\\{y=-\frac{16}{9}}\end{array}\right.$,
∴当点P坐标(-$\frac{4}{3}$,-$\frac{16}{9}$)时,∠PAO=∠BCO.
点评 本题考查二次函数综合题、待定系数法、等腰直角三角形性质,一次函数等知识,解题的关键是构建一次函数,学会利用方程组求函数交点坐标,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
| A. |  | B. |  | C. |  | D. |  |
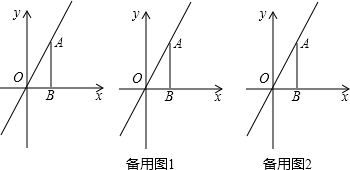
 如图,已知抛物线y=-x2通过平移后得到…,y1=-(x-1)2+2,y2=-(x-2)2+4,y3=-(x-3)2+6,…,平移后的顶点…,P1,P2,P3,…Pk(k为整数)依次都在格点上,这些抛物线称为“好顶点抛物线”.
如图,已知抛物线y=-x2通过平移后得到…,y1=-(x-1)2+2,y2=-(x-2)2+4,y3=-(x-3)2+6,…,平移后的顶点…,P1,P2,P3,…Pk(k为整数)依次都在格点上,这些抛物线称为“好顶点抛物线”. 如图所示,已知抛物线y=ax2-4x-5(a>0,a为常数)与一次函数y=$\frac{1}{2}$x+b(b为常数)交于点M(6,n),直线y=$\frac{1}{2}$x+b与x轴及y轴交于两点A、B,△AOB的周长是12+4$\sqrt{5}$,抛物线y=ax2-4x-5与y轴交于点C,与x轴交于点D、E(点E在点D的右侧).
如图所示,已知抛物线y=ax2-4x-5(a>0,a为常数)与一次函数y=$\frac{1}{2}$x+b(b为常数)交于点M(6,n),直线y=$\frac{1}{2}$x+b与x轴及y轴交于两点A、B,△AOB的周长是12+4$\sqrt{5}$,抛物线y=ax2-4x-5与y轴交于点C,与x轴交于点D、E(点E在点D的右侧).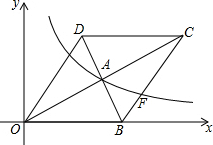 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).