题目内容
20.我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.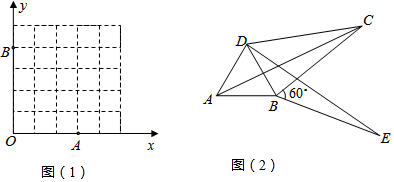
(1)写出你所学过的特殊四边形中是勾股四边形的两种图形的名称矩形,正方形;
(2)如图1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标.
(3)如图2,将△ABC绕顶点B按顺时针方向旋转60°,得到△DBE,连接AD、DC,∠DCB=30°.求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
(4)若将图2中△ABC绕顶点B按顺时针方向旋转a度(0°<a<90°),得到△DBE,连接AD、DC,则∠DCB=($\frac{1}{2}$α)°,四边形BECD是勾股四边形.
分析 (1)根据勾股四边形的定义,可知正方形、矩形直角梯形都是勾股四边形;
(2)如图1中,以OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标为(3,4)或(4,3);
(3)如图2,连接CE,只要证明△DCE是直角三角形即可解决问题.
(4)如图3,当∠DCB=$\frac{1}{2}$α,四边形BECD是勾股四边形.连接CE,只要证明△DCE是直角三角形即可解决问题.
解答 解:(1)矩形,正方形;
故答案为矩形,正方形;
(2)如图1所示:M(3,4),M(4,3); 
(3)证明:如图2,连接CE,
由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,
又∵∠CBE=60°,
∴△CBE为等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=∠DCB+∠BCE=30°+60°=90°,
∴DC2+EC2=DE2,
∴DC2+BC2=AC2.
∴即四边形ABCD是勾股四边形.
(4)如图3,当∠DCB=$\frac{1}{2}$α,四边形ABCD是勾股四边形.
理由:连接CE,
由旋转得:△ABC≌△DBE,
∴AC=DE,BC=BE,
又∵∠CBE=α,
∴∠BCE=∠BEC=90°-$\frac{1}{2}$α,
∴∠DCE=90°,
∴DC2+EC2=DE2,
∴即四边形BECD是勾股四边形.
故答案为:$\frac{1}{2}$α.
点评 本题考查四边形综合题、勾股定理、等边三角形的判定和性质、等腰三角形的性质、全等三角形的判定和性质等知识,解题的关键是理解题意,正确寻找全等三角形解决问题,属于中考压轴题.

练习册系列答案
相关题目
10.下列四边形中,是轴对称图形但不是中心对称图形的是( )
| A. | 等腰梯形 | B. | 平行四边形 | C. | 菱形 | D. | 矩形 |
11.据初步统计,2017年春节期间,安徽省累计接待游客2681.52万人次,实现旅游总收入142亿元,其中142亿用科学记数法表示为( )
| A. | 1.42×108 | B. | 1.42×109 | C. | 1.42×1010 | D. | 1.42×1011 |
8.计算(x-1)(2x+1)-(x2+x-2)的结果,与下列哪一个式子相同( )
| A. | x2-2x-3 | B. | x2-2x+1 | C. | x2+x-3 | D. | x2-3 |
12.已知直线y=mx与双曲线y=$\frac{k}{x}$的一个交点坐标为(2,4),则它们的另一个交点坐标是( )
| A. | (-2,4) | B. | (-4,-2) | C. | (4,2) | D. | (-2,-4) |
11.若把分式$\frac{2x}{x-y}$中x、y的都扩大5倍,则分式的值( )
| A. | 扩大5倍 | B. | 扩大10倍 | C. | 不变 | D. | 缩小到原来的$\frac{1}{5}$ |
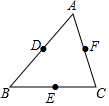 如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中能画平行四边形的个数是( )
如图,在△ABC中,D,E,F分别是AB,BC,CA的中点,以这些点为顶点,在图中能画平行四边形的个数是( )