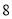��Ŀ����
��ͼ����O��Rt��ABC�����Բ����ABC=90�㣬��BD=BA��AC=13��BC=5��BE��DC��DC���ӳ����ڵ�E��

��1����֤��CB�ǡ�ECA�Ľ�ƽ���ߣ�
��2����DE�ij���
��3����֤��BE�ǡ�O�����ߣ�
��1��֤������������2������3��֤���������� �������� �����������1������BD=BA�ó���BDA=��BAD�����ɡ�BCA=��BDA���ɵó����ۣ� ��2���жϡ�BED�ס�CBA�����ö�Ӧ�߳ɱ��������ʿ����DE�ij��ȣ� ��3������OB��OD��֤����ABO�ա�DBO���Ƴ�OB��DE���̶��ж�BE��OB���ɵó����ۣ� �����������1����BD=BA�� ���BDA=��B...
��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ


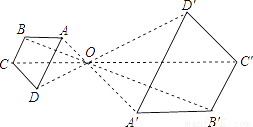
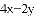
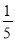 abc+
abc+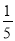 ab2��a2bc��һ����ʽ�ǩ�
ab2��a2bc��һ����ʽ�ǩ�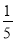 ab����ô��һ����ʽ�ǣ�������
ab����ô��һ����ʽ�ǣ�������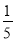 ac D. c+b��
ac D. c+b��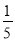 ac
ac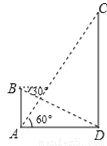
 ��������
�������� ��
�� 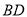 ���ڵ�
���ڵ�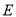 ��
��

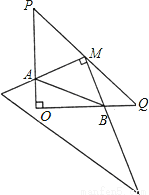
 ����ͼ
����ͼ ����֤��
����֤�� 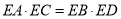 ��
�� ����ͼ
����ͼ ������
������ ��
��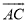 �е㣬
�е㣬 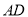 �ǡ�
�ǡ� ֱ����
ֱ���� 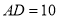 ��
�� 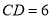 ��
��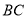 �ij���
�ij���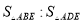 ��
��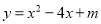 �Ķ�����
�Ķ�����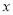 ���ϣ���
���ϣ���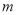 ��ֵΪ�� ����
��ֵΪ�� ����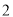 B.
B. 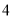 C.
C. 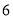 D.
D.