题目内容
在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.
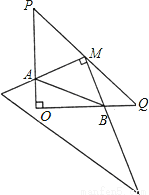
(1)求证:MA=MB;
(2)连结AB,探究:在旋转三角尺的过程中,△AOB的周长是否存在最小值?若存在,求出最小值;若不存在,请说明理由.
(1)证明见解析;(2)有最小值,最小值为4+2. 【解析】 试题分析:(1)过点M作ME⊥OP于点E,作MF⊥OQ于点F,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得∠AME=∠BMF,再利用“角边角”证明△AME和△BMF全等,根据全等三角形对应边相等即可证明; (2)根据全等三角形对应边相等可得AE=BF,设OA=x,表示出AE为...
练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目


 B.
B.  C.
C. 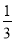 D.
D. 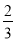
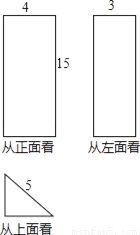

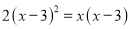
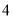 个收费通道
个收费通道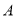 、
、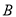 、
、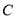 、
、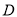 中,可随机选择其中的一个通过.
中,可随机选择其中的一个通过.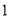 )一辆车经过此收费站时,选择
)一辆车经过此收费站时,选择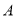 通道通过的概率是__________.
通道通过的概率是__________.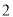 )用树状图或列表法两辆车经过此收费站时,选择不同通道通过的概率.
)用树状图或列表法两辆车经过此收费站时,选择不同通道通过的概率.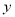 是关于
是关于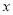 的二次函数的是( ).
的二次函数的是( ).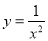 B.
B. 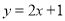 C.
C. 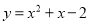 D.
D. 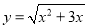
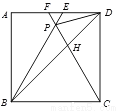
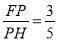 ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④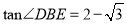 . 其中正确的是( ).
. 其中正确的是( ).