题目内容
7.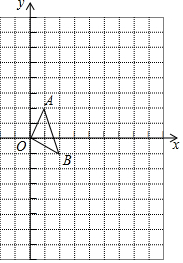 如图,在正方形网格中,每一个小正方形的边长都为1,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).
如图,在正方形网格中,每一个小正方形的边长都为1,△OAB的顶点分别为O(0,0),A(1,2),B(2,-1).(1)以点O(0,0)为位似中心,按位似比1:3在位似中心的同侧将△OAB放大为△OA′B′,放大后点A、B的对应点分别为A′、B′,请在图中画出△OA′B′;
(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C'的坐标(3a,3b);
(3)直接写出四边形ABA′B′的面积是20.
分析 (1)利用位似图形的性质得出对应点位置进而求出即可;
(2)利用位似图形的性质结合位似比进而求出即可;
(3)先后求出S△A′OB′、S△AOB,继而根据S四边形ABA′B′=S△A′OB′-S△AOB可得.
解答 解:(1)如图,△OA′B′即为所求作三角形;
(2)∵点A(1,2)的对应点A′的坐标:(3,6),点B(2,-1)的对应点B′的坐标:(6,-3);
∴点C(a,b)的对应点C'的坐标为:(3a,3b);
故答案为:(3a,3b);
(3)∵OA=OB=$\sqrt{5}$,AB=$\sqrt{10}$,
∴OA2+OB2=AB2,
∴△AOB为等腰直角三角形,
则S△AOB=$\frac{1}{2}$OA•OB=$\frac{5}{2}$,
同理可得S△A′OB′=$\frac{1}{2}$OA′•OB′=$\frac{45}{2}$,
∴四边形ABA′B′的面积是S△A′OB′-S△AOB=20,
故答案为:20.
点评 此题主要考查了位似变换,根据题意得出对应点位置是解题关键.

练习册系列答案
相关题目
15.三角形两边长分别为2和4,第三边长是方程x(x-4)-2(x-4)=0的解,则这个三角形周长为( )
| A. | 8 | B. | 8和10 | C. | 10 | D. | 8 或10 |
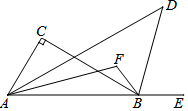 如图,Rt△ABC中,∠C=90°,AD平分∠BAC,BD平分∠CBE,AF平分∠DAB,BF平分∠ABD,则∠F=112.5°.
如图,Rt△ABC中,∠C=90°,AD平分∠BAC,BD平分∠CBE,AF平分∠DAB,BF平分∠ABD,则∠F=112.5°.