题目内容

15．三角形两边长分别为2和4，第三边长是方程x（x-4）-2（x-4）=0的解，则这个三角形周长为（　　）
A．8B．8和10C．10D．8 或10

分析 先求出方程的解，得出三角形的三边长，看看是否能组成三角形，最后求出即可．

解答 解：x（x-4）-2（x-4）=0，
解得：x=4或2，
①三角形的三边为2、2、4时，不符合三角形三边关系定理，此时不能组成三角形；
②三角形的三边为2、4、4时，符合三角形三边关系定理，此时能组成三角形，组成的三角形周长为2+4+4=10，
故选C．

点评 本题考查了解一元二次方程，三角形三边关系定理的应用，能求出符合的所有情况是解此题的关键．

练习册系列答案
相关题目
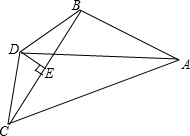5．如图，在△ABC中，AC＞AB，AD平分∠BAC，点D到点B与点C的距离相等，过点D作DE⊥BC于点E．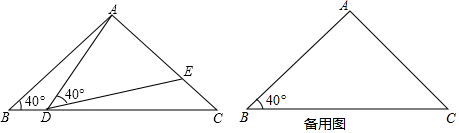
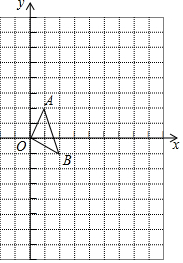（1）求证：BE=CE；
（2）请直接写出∠ABC，∠ACB，∠ADE三者之间的数量关系：∠ABC-∠ACB=2∠ADE
（3）若∠ACB=40°，∠ADE=20°，求∠DCB的度数．
6．如图，在△ABC中，AB=AC=4，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．
（1）当∠BDA=115°时，∠EDC=25°，∠DEC=115°；
（2）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，求出∠BDA的度数．若不可以，请说明理由．
3．近年来，地震、泥石流等自然灾害频繁发生，造成极大的生命和财产损失．为了更好地做好“防震减灾”工作，我市相关部门对某中学学生“防震减灾”的知晓率采取随机抽样的方法进行问卷调查，调查结果分为“非常了解”、“比较了解”、“基本了解”和“不了解”四个等级．小明根据调查结果绘制了如图统计图，请根据提供的信息回答问题：

（1）本次调查中，样本容量是400；
（2）扇形统计图中“基本了解”部分所对应的扇形圆心角是144°；在该校2000名学生中随机提问一名学生，对“防震减灾”不了解的概率的估计值为$\frac{1}{20}$；
（3）请补全频数分布直方图．
10．已知a、b互为相反数且a≠0，c、d互为倒数，m的绝对值是最小的正整数，求m+$\frac{2010（a+b）}{2011}$-cd的值．
20．在数$\frac{4}{5}$、-$\sqrt{11}$、0.$\stackrel{•}{7}$、-π、$\root{3}{27}$、0.1010010001…（相邻两个1之间依次多一个0）中，无理数有（　　）个．
A．1B．2C．3D．4
7．如图，在正方形网格中，每一个小正方形的边长都为1，△OAB的顶点分别为O（0，0），A（1，2），B（2，-1）．
（1）以点O（0，0）为位似中心，按位似比1：3在位似中心的同侧将△OAB放大为△OA′B′，放大后点A、B的对应点分别为A′、B′，请在图中画出△OA′B′；
（2）在（1）中，若C（a，b）为线段AB上任一点，写出变化后点C的对应点C'的坐标（3a，3b）；
（3）直接写出四边形ABA′B′的面积是20．
4．已知：|m|=3，|n|=4，若m＞n，则m-n的值为7或1．
5．如图，AD是△ABC的角平分线，E在CB的延长线上，且DE=CD，EF∥AC交AB的延长线于F，求证：AF+EF=AC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网