��Ŀ����
12��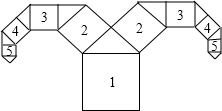 ������
������������ũ�����꣮��ͼ��ʾ��һ�֡���ͷ����ͼ�����������ǣ���������1��ʼ��������һ��Ϊб�ߣ�����������ֱ�������Σ�Ȼ��������ֱ�DZ�Ϊ�ߣ��ֱ�������������2��3��4��L����2�䡢3�䡢4�䡢L���������ƣ�
��1��̽��������1��������2������������2�䣩�߳���������ϵ��������2��������3������������3�䣩�߳���������ϵ�������ǵ�������ϵ�������Ĺ����ԣ�
��2��������1��������n������������n�䣩�߳����������кι�ϵ����������1�ı߳�Ϊa����������n������������n�䣩�߳�����α�ʾ��
��3����������7�ı߳�Ϊ1cm����������1�ı߳����
���� ��1����������2�ı߳�Ϊx��������1�ı߳�Ϊa���ɹ��ɶ����ó�x2+x2=a2��������ɣ�
��2�����ݣ�1��������Ľ�����ɵó��𰸣�
��3�����ݵó��Ĺ��ɼ�������𰸣�
��� �⣺��1����������2�ı߳�Ϊx��������1�ı߳�Ϊa��
���ɹ��ɶ����ã�x2+x2=a2��
��ã�a=$\sqrt{2}$x��
��������1�ı߳���������2������������2�䣩�߳���$\sqrt{2}$����
ͬ��������2�ı߳���������3������������3�䣩�߳���$\sqrt{2}$����
������1�ı߳���������2������������2�䣩�߳���$\sqrt{2}$����
����������1�ı߳���������n������������n�䣩�߳��ģ�$\sqrt{2}$��n-1����
��2��������1��������n������������n�䣩�߳��������ϵĹ�ϵ�ǣ�������1�ı߳���������n������������n�䣩�߳��ģ�$\sqrt{2}$��n-1����
������1�ı߳�Ϊa����������n������������n�䣩�߳���ʾΪ$\frac{a}{��\sqrt{2}��^{n-1}}$��
��3����������1�ı߳���������n������������n�䣩�߳��ģ�$\sqrt{2}$��n-1����
�൱������7�ı߳�Ϊ1cmʱ��������1�ı߳�Ϊ1����$\sqrt{2}$��7-1=8��cm����
���� ���⿼���������ε����ʡ�����ֱ�������ε����ʡ����ɶ�����Ӧ�ã�����Ĺؼ����ܸ�������Ľ���ó����ɣ�ע�⣺ֱ�������ε���ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ����

 ��У����ϵ�д�
��У����ϵ�д�| A�� | x+y=18 | B�� | x+y=36 | C�� | 4x+2y=36 | D�� | 2x+4y=36 |
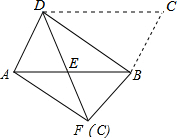 ��ͼ����ƽ���ı���ABCD�ضԽ���BD�����۵����۵����C���ڵ�F����DF��AB�ڵ�E��
��ͼ����ƽ���ı���ABCD�ضԽ���BD�����۵����۵����C���ڵ�F����DF��AB�ڵ�E��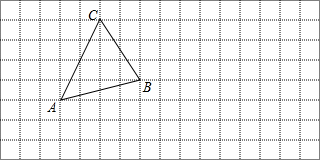
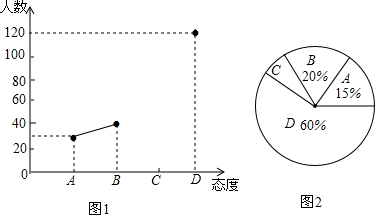
 ��֪������ABC����DΪ��Bƽ�ƺ�Ķ�Ӧ�㣬����D��������ABCƽ�ƺ��ͼ�Σ�
��֪������ABC����DΪ��Bƽ�ƺ�Ķ�Ӧ�㣬����D��������ABCƽ�ƺ��ͼ�Σ�