题目内容
17.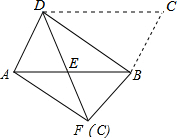 如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.(1)求证;∠EDB=∠EBD;
(2)判断AF与DB是否平行,并说明理由.
分析 (1)由折叠和平行线的性质易证∠EDB=∠EBD;
(2)AF∥DB;首先证明AE=EF,得出∠AFE=∠EAF,然后根据三角形内角和与等式性质可证明∠BDE=∠AFE,所以AF∥BD.
解答 解:(1)由折叠可知:∠CDB=∠EDB,
∵四边形ABCD是平行四边形,
∴DC∥AB,
∴∠CDB=∠EBD,
∴∠EDB=∠EBD;
(2)AF∥DB;
∵∠EDB=∠EBD,
∴DE=BE,
由折叠可知:DC=DF,
∵四边形ABCD是平行四边形,
∴DC=AB,
∴DF=AB,
∴AE=EF,
∴∠EAF=∠EFA,
在△BED中,∠EDB+∠EBD+∠DEB=180°,
∴2∠EDB+∠DEB=180°,
同理,在△AEF中,2∠EFA+∠AEF=180°,
∵∠DEB=∠AEF,
∴∠EDB=∠EFA,
∴AF∥DB.
点评 本题主要考查了折叠变换、平行四边形的性质、等腰三角形的性质的综合应用,运用三角形内角和定理和等式性质得出内错角相等是解决问题的关键.

练习册系列答案
相关题目
8.如图,甲、乙、丙三个图形都是由大小相同的小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数.其中主视图相同的是( )
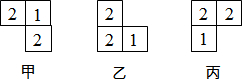
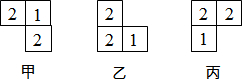
| A. | 仅有甲和乙相同 | B. | 仅有甲和丙相同 | C. | 仅有乙和丙相同 | D. | 甲、乙、丙都相同 |
5.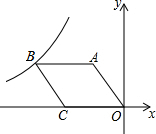 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B,则k的值为( )
 如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B,则k的值为( )
如图,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=$\frac{k}{x}$(x<0)的图象经过顶点B,则k的值为( )| A. | -12 | B. | -27 | C. | -32 | D. | -36 |
2. 有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )
有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )
 有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )
有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )| A. |  | B. |  | C. |  | D. |  |
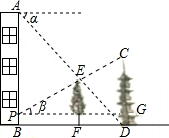 如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)
如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号) 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于60度.
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于60度.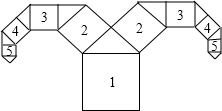 附加题
附加题