题目内容
1.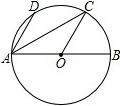 如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )
如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )| A. | 4 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{6}$ |
分析 连接BC,根据等腰三角形的性质得到∠CAO=∠ACO,根据平行线的性质得到∠DAC=∠ACO,等量代换得到∠DAC=∠CAB,根据直角三角形的性质即可得到结论.
解答 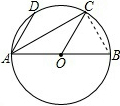 解:连接BC,
解:连接BC,
∵OA=OC,
∴∠CAO=∠ACO,
∵AD∥OC,
∴∠DAC=∠ACO,
∴∠DAC=∠CAB,
∵∠DAB=60°,
∴∠CAB=$\frac{1}{2}$∠DAB=30°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AB=4,
∴AC=$\frac{\sqrt{3}}{2}$AB=2$\sqrt{3}$.
故选C.
点评 本题考查了圆的认识,平行线的性质,含30°角的直角三角形的性质,属于基础题,比较简单.

练习册系列答案
相关题目
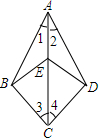 已知:如图,∠1=∠2,∠3=∠4.求证:∠AEB=∠AED.
已知:如图,∠1=∠2,∠3=∠4.求证:∠AEB=∠AED.
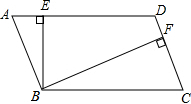 如图,平行四边形ABCD中,BE⊥AD于E,BF⊥CD于F,BE=2,BF=3,平行四边形ABCD的周长为20,则平行四边形ABCD的面积为12.
如图,平行四边形ABCD中,BE⊥AD于E,BF⊥CD于F,BE=2,BF=3,平行四边形ABCD的周长为20,则平行四边形ABCD的面积为12.