题目内容
12.计算:$\frac{2}{tan60°+1}-{(\sqrt{3}-1)^0}$+2sin60°-3tan30°.分析 先利用特殊角的三角函数值和零指数幂的意义得到原式=$\frac{2}{\sqrt{3}+1}$-1+2×$\frac{\sqrt{3}}{2}$-3×$\frac{\sqrt{3}}{3}$,然后利用二次根式的乘除法则运算即可.
解答 解:原式=$\frac{2}{\sqrt{3}+1}$-1+2×$\frac{\sqrt{3}}{2}$-3×$\frac{\sqrt{3}}{3}$
=$\sqrt{3}$-1-1+$\sqrt{3}$-$\sqrt{3}$
=$\sqrt{3}$-2.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂.

练习册系列答案
相关题目
1.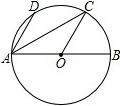 如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )
如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )
 如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )
如图,AB是⊙O的直径,AB=4,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则AC=( )| A. | 4 | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{6}$ |
2.若(1-2x)0=1,则( )
| A. | x≠0 | B. | x≠2 | C. | x≠$\frac{1}{2}$ | D. | x为任意有理数 |
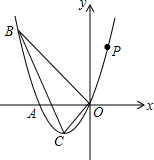 如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C.