题目内容
9.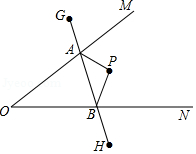 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为14,则△PAB的周长为14.
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点.若GH的长为14,则△PAB的周长为14.
分析 先根据轴对称的性质得出PA=AG,PB=BH,由此可得出结论.
解答 解:∵P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,
∴PA=AG,PB=BH,
∴△PAB的周长=AP+PB+AB=AG+AB+BH=GH=14.
故答案为:14.
点评 本题考查的是轴对称的性质,熟知如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )| A. | 5.5 | B. | 4 | C. | 4.5 | D. | 3 |
19. 如图所示,有一块直角三角形纸片,两直角边分别为:AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图所示,有一块直角三角形纸片,两直角边分别为:AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
 如图所示,有一块直角三角形纸片,两直角边分别为:AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图所示,有一块直角三角形纸片,两直角边分别为:AC=5cm,BC=12cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | $\frac{10}{3}$cm | B. | 8cm | C. | $\frac{8}{3}$cm | D. | 4cm |
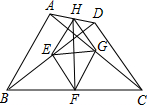 如图,四边形ABCD,AD与BC不平行,AB=CD.AC,BD为四边形ABCD的对角线.E,F,G,H分别是BD,BC,AC,AD的中点.
如图,四边形ABCD,AD与BC不平行,AB=CD.AC,BD为四边形ABCD的对角线.E,F,G,H分别是BD,BC,AC,AD的中点.


