Question

15．如图，等边△ABC的边长是4，D，E分别为AB，AC的中点，延长BC至点F，使CF=$\frac{1}{2}$BC，连接CD和EF．
（1）求证：DE=CF；
（2）求EF的长；
（3）求四边形DEFC的面积．

Answer 1

分析 （1）利用三角形中位线定理即可解决问题．
（2）先求出CD，再证明四边形DEFC是平行四边形即可．
（3）过点D作DH⊥BC于H，求出CF、DH即可解决问题．

解答 解：（1）在△ABC中，
∵D、E分别为AB、AC的中点，
∴DE为△ABC的中位线，
∴DE=$\frac{1}{2}$BC，
∵CF=$\frac{1}{2}$BC，
∴DE=CF．

（2）∵AC=BC，AD=BD，
∴CD⊥AB，
∵BC=4，BD=2，
∴CD=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$，
∵DE∥CF，DE=CF，
∴四边形DEFC是平行四边形，
∴EF=CD=2$\sqrt{3}$．

（3）过点D作DH⊥BC于H．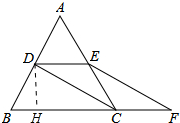

∵∠DHC=90°，∠DCB=30°，
∴DH=$\frac{1}{2}$DC=$\sqrt{3}$，
∵DE=CF=2，
∴S_{四边形DEFC}=CF•DH=2×$\sqrt{3}$=2$\sqrt{3}$．

点评 本题考查等边三角形的性质、三角形中位线定理、勾股定理、平行四边形的判定和性质等知识，解题的关键是灵活应用这些知识解决问题，记住平行四边形的面积公式，学会添加常用辅助线，属于中考常考题型．