题目内容
8. 已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.
已知:如图,AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.(1)求证:DE为⊙O的切线.
(2)求证:DF2=BF•AF.
分析 (1)连AD,OD,则∠ADB=∠ADC=90°,由直角三角形斜边上的中线性质得:EA=ED,∠EDA=∠EAD,由等腰三角形的性质得:∠ODA=∠OAD,证得∠EDO=∠EAO,即可得出结论;
(2)证明:由切线的性质得:∠ODF=∠FDB+∠ODB=∠FAD+∠OBD=90°,证出∠FDB=∠FAD,∠F为公共角,得出△FDB∽△FAD,由对应边成比例即可得出结论.
解答 (1)证明:连AD,OD,如图所示: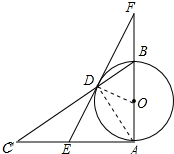
∵AB为⊙O的直径,
∴∠ADB=∠ADC=90°,
∵E是AC的中点,
∴EA=ED,
∴∠EDA=∠EAD,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠EDO=∠EAO,
∵AB⊥AC,
∴∠EAO=90°,
∴∠EDO=90°,
∴DE为⊙O的切线;
(2)证明:∵DE为⊙O的切线,
∴∠ODF=∠FDB+∠ODB=∠FAD+∠OBD=90°,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠FDB=∠FAD,
又∵∠F为公共角,
∴△FDB∽△FAD,
∴$\frac{DF}{AF}$=$\frac{BF}{DF}$,
∴DF2=BF•AF.
点评 本题考查了相似三角形的判定与性质、切线的判定与性质、直角三角形斜边上的中线性质、等腰三角形的性质等知识;熟练掌握切线的判定与性质、相似三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
13.据研究,一种H7N9病毒直径为30纳米(1纳米=10-9米).下列用科学记数法表示这个病毒直径的大小,正确的是( )
| A. | 30×10-9米 | B. | 3.0×10-8米 | C. | 3.0×10-10米 | D. | 0.3×10-7米 |
17.一个圆锥的侧面展开图是半径为8cm,圆心角为120°的扇形,则这个圆锥的底面半径为( )
| A. | $\frac{16}{3}\sqrt{2}$ | B. | $\frac{16}{3}$cm | C. | $\frac{8}{3}\sqrt{2}$cm | D. | $\frac{8}{3}$cm |
 矩形ABCD中,AB=5,BC=4,将矩形折叠,使得点B落在线段CD的点F处,则线段BE的长为2.5.
矩形ABCD中,AB=5,BC=4,将矩形折叠,使得点B落在线段CD的点F处,则线段BE的长为2.5.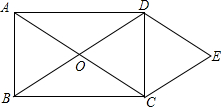 如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.