题目内容
3. 如图,在四边形ABCD中,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=3,BC=5.
如图,在四边形ABCD中,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,若AD=3,BC=5.(1)求证:AE=BE;
(2)求EF的长.
分析 (1)先根据折叠的性质得EA=EF,BE=EF,等量代换得到结论;
(2)根据折叠的性质得到DF=AD=3,CF=CB=5,则AB=2EF,DC=8,再作DH⊥BC于H,由于AD∥BC,∠B=90°,则可判断四边形ABHD为矩形,所以DH=AB=2EF,HC=BC-BH=BC-AD=2,然后在Rt△DHC中,利用勾股定理计算出DH=2$\sqrt{15}$,所以EF=$\sqrt{15}$.
解答 解: ∵分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,
∵分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,
∴EA=EF,BE=EF,
∴AE=BE;
(2)∵分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边的点F处,
∴DF=AD=3,CF=CB=5,
∴AB=2EF,DC=DF+CF=8,
作DH⊥BC于H,
∵AD∥BC,∠B=90°,
∴四边形ABHD为矩形,
∴DH=AB=2EF,HC=BC-BH=BC-AD=5-3=2,
在Rt△DHC中,DH=$\sqrt{D{C}^{2}-H{C}^{2}}$=2$\sqrt{15}$,
∴EF=$\frac{1}{2}$DH=$\sqrt{15}$.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
18.下列计算正确的是( )
| A. | (-$\frac{4}{3}$ab)(-3ab)2=12a2b2 | B. | (xy)8÷(xy)2=x4y4 | ||
| C. | x10÷(x7÷x2)=x5 | D. | (-4a-1)(4a-1)=16a2-1 |
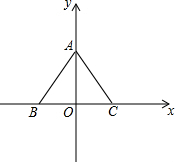 如图,△ABC在平面直角坐标系中的位置如图所示,若S△ABC=12,BC=2OC,且AC,BC的长满足$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$.
如图,△ABC在平面直角坐标系中的位置如图所示,若S△ABC=12,BC=2OC,且AC,BC的长满足$\left\{\begin{array}{l}{BC-AC=1}\\{BC+AC=11}\end{array}\right.$.
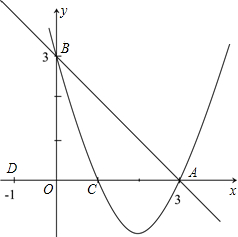 如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.
如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.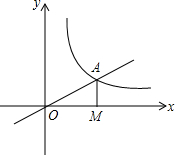 如图所示,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为M,已知△OAM的面积为1.
如图所示,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为M,已知△OAM的面积为1.