题目内容
13．
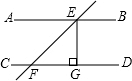如图，已知直线AB∥CD，直线EF截AB、CD于E、F，EG⊥CD，∠EFD=45°且FG=6，则AB、CD之间的距离为6．
分析 根据图形得出EG的长是AB、CD之间的距离，根据垂直定义得出∠EGF=90°，求出∠EFG=45°，推出FG=EG，即可得出答案．
解答 解：∵EG⊥CD，AB∥CD，
∴EG⊥AB，
即EG的长是AB、CD之间的距离，
∵EG⊥CD，
∴∠EGF=90°，
∵∠EFG=45°，
∴∠FEG=180°-90°-4°=45°=∠EFG，
∴EG=FG=6，
即AB、CD之间的距离是6．
故答案为：6．
点评 本题考查了平行线间的距离，等腰三角形的判定，三角形的内角和定理等知识点，关键是得出EG的长是AB、CD之间的距离和求出EG的长．
练习册系列答案
相关题目
如图，△ABC的∠B与∠C的外角平分线相交于D点，∠A=50°，则∠D=75°．
如图，破残的圆形轮片上，弦AB的垂直平分线交弧AB于C，交弦AB于D．求作此残片所在的圆（不写作法，保留作图痕迹）．
5．比较$\sqrt{2}$和$\frac{\sqrt{5}}{2}$的大小（ ）
| A． | $\sqrt{2}$≥$\frac{\sqrt{5}}{2}$ | B． | $\sqrt{2}$≤$\frac{\sqrt{5}}{2}$ | C． | $\sqrt{2}$＞$\frac{\sqrt{5}}{2}$ | D． | $\sqrt{2}$＜$\frac{\sqrt{5}}{2}$ |