题目内容
15．小虫从原点O出发沿数轴来回爬行，规定向右爬行的路程记为正数，向左爬行的路程记为负数，爬行过的路程依次为：（单位：厘米）+5，-3，+10，-8，-6，+12，-10．问小虫最后是否回到出发点O？在爬行的过程中，如果每爬1厘米奖励一粒芝麻，则小虫可共得多少粒芝麻？分析 把记录数据相加，结果为0，说明小虫最后回到出发点A；小虫一共得到的芝麻数，与它爬行的方向无关，只与爬行的距离有关，所以应把绝对值相加，再求得到的芝麻粒数．
解答 解：+5-3+10-8-6+12-10=27-27=0．
所以小虫最后回到出发点A；
小虫爬行的总路程为：|+5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10|=5+3+10+8+6+12+10=54（cm）．
所以小虫一共得到54粒芝麻．
点评 本题主要考查的是有理数的加法和应用，明确距离即绝对值与正负无关是解题的关键．
练习册系列答案
相关题目
5．若关于x的方程$\frac{x-1}{x-2}-\frac{m}{2-x}$=m无解，则m的值为（ ）
| A． | 0 | B． | -1 | C． | 0或-1 | D． | 1或-1 |
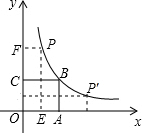如图，正方形OABC的面积为16，点O为坐标原点，点B在双曲线y=$\frac{k}{x}$（x＞0）上，点P（m，n）是双曲线上任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E、F，并设矩形OEPF在正方形OABC之外部分的面积为S．
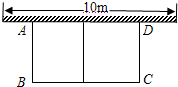如图，一面利用墙，用总长度为24m的篱笆围成矩形花圃ABCD，其中中间用一段篱笆隔成两个小矩形，墙可利用的最大长度为10m，设AB的长为xm，矩形花圃ABCD的面积为ym2．
5．比较$\sqrt{2}$和$\frac{\sqrt{5}}{2}$的大小（ ）
| A． | $\sqrt{2}$≥$\frac{\sqrt{5}}{2}$ | B． | $\sqrt{2}$≤$\frac{\sqrt{5}}{2}$ | C． | $\sqrt{2}$＞$\frac{\sqrt{5}}{2}$ | D． | $\sqrt{2}$＜$\frac{\sqrt{5}}{2}$ |