题目内容
10.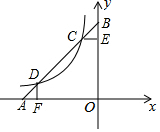 如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=-$\frac{5}{x}$(x<0)交于C,D两点,点C的横坐标为-1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法:①b=6;②BC=AD;③五边形CDFOE的面积为35;④当x<-1时,y1>y2,其中正确的有( )
如图,直线y1=x+b与x轴、y轴分别交于A,B两点,与反比例函数y2=-$\frac{5}{x}$(x<0)交于C,D两点,点C的横坐标为-1,过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F.下列说法:①b=6;②BC=AD;③五边形CDFOE的面积为35;④当x<-1时,y1>y2,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 首先把x=-1代入反比例函数解析式,求得C的坐标,把C的坐标代入直线解析式即可求得b的值;
根据轴对称图形的性质即可证得BC=AD;
求得D的坐标,作CG⊥x轴于点G.根据S五边形CDFOE=S梯形CDFG+S矩形CGOE求解,即可对③进行判断;
根据函数图象可以对④判断.
解答 解:把x=-1代入y2=-$\frac{5}{x}$得y=5,则C的坐标是(-1,5),
把(-1,5)代入y1=x+b得-1+b=5,
解得b=6,故①正确;
反比例函数y2=-$\frac{5}{x}$和y1=x+6都关于第二、四象限的平分线对称,则BC=AD,故②正确;
根据题意得$\left\{\begin{array}{l}{y=x+6}\\{y=-\frac{5}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-1}\\{y=5}\end{array}\right.$或$\left\{\begin{array}{l}{x=-5}\\{y=1}\end{array}\right.$,
则D的坐标是(-5,1).
作CG⊥x轴于点G.
则S五边形CDFOE=S梯形CDFG+S矩形CGOE=$\frac{1}{2}$(1+5)(5-1)+1×5=12+5=17,故③错误;
当x<-5时,y1<y2,故④错误.
故选B.
点评 本题考查了待定系数法求函数的解析式,以及函数图象的交点,正确求得D的坐标是关键.

练习册系列答案
相关题目
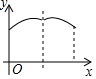
15. 如图所示的图象中所反映的过程是:王强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示王强离家的距离.以下四个说法错误的是( )
如图所示的图象中所反映的过程是:王强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示王强离家的距离.以下四个说法错误的是( )
 如图所示的图象中所反映的过程是:王强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示王强离家的距离.以下四个说法错误的是( )
如图所示的图象中所反映的过程是:王强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示王强离家的距离.以下四个说法错误的是( )| A. | 体育场离王强家2.5千米 | |
| B. | 王强在体育场锻炼了15分钟 | |
| C. | 体育场离早餐店4千米 | |
| D. | 王强从早餐店回家的平均速度是3千米/小时 |
 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,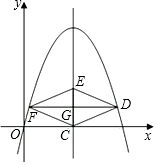 如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.
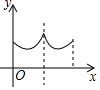
如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点. 如图,一个寻宝游戏的寻宝结构是等边三角形ABC及中心O,通道是AB,BC,CA,OA,OB,OC组成.为记录寻宝者的进行路线,将定位仪放置在BC的中点M处,寻宝者的行进路线为B→O→C,若寻宝者匀速行进,设寻宝者行进的时间为x,寻宝者与定位仪之间的距离为y,则y与x的函数关系的图象大致可能为( )
如图,一个寻宝游戏的寻宝结构是等边三角形ABC及中心O,通道是AB,BC,CA,OA,OB,OC组成.为记录寻宝者的进行路线,将定位仪放置在BC的中点M处,寻宝者的行进路线为B→O→C,若寻宝者匀速行进,设寻宝者行进的时间为x,寻宝者与定位仪之间的距离为y,则y与x的函数关系的图象大致可能为( )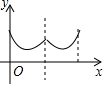
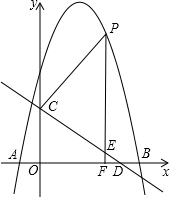 如图,抛物线y=ax2+bx+5与x轴交于A(-1,0)、B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是抛物线上一动点,过点P作直线PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
如图,抛物线y=ax2+bx+5与x轴交于A(-1,0)、B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是抛物线上一动点,过点P作直线PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m. 如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AC的延长线于F,E为垂足.则结论:(1)AD=BF;(2)CF=CD;(3)AC+CD=AB;(4)BE=CF;(5)BF=2BE,其中正确的结论个数是( )
如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AC的延长线于F,E为垂足.则结论:(1)AD=BF;(2)CF=CD;(3)AC+CD=AB;(4)BE=CF;(5)BF=2BE,其中正确的结论个数是( )