题目内容
16．关于x，y的二元一次方程组$\left\{\begin{array}{l}x+y=9k\\ x-y=5k\end{array}\right.$的解也是二元一次方程2x+3y=6的解，则k的值为（ ）| A． | $\frac{3}{10}$ | B． | $\frac{10}{3}$ | C． | $-\frac{3}{10}$ | D． | $-\frac{10}{3}$ |
分析 先求出方程组的解，把x、y的值代入方程2x+3y=6，即可求出k．
解答 解：解方程组$\left\{\begin{array}{l}x+y=9k\\ x-y=5k\end{array}\right.$得：$\left\{\begin{array}{l}{x=7k}\\{y=2k}\end{array}\right.$，
∵关于x，y的二元一次方程组$\left\{\begin{array}{l}x+y=9k\\ x-y=5k\end{array}\right.$的解也是二元一次方程2x+3y=6的解，
∴代入得：14k+6k=6，
解得：k=$\frac{3}{10}$，
故选A．
点评 本题考查了解二元一次方程组，二元一次方程组的解，解一元一次方程等知识点，能得出关于k的方程是解此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
4．若分式$\frac{x-2}{x-3}$有意义，则x满足的条件是（ ）
| A． | x≠0 | B． | x≠2 | C． | x≠3 | D． | x≥3 |
在?ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF=BE，连接AF，BF．
1．某工厂承接了一批纸箱加工任务，用如图1所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不计）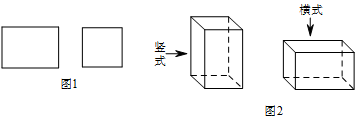
（1）若该厂购进正方形纸板1000张，长方形纸板2000张，问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完．
分析：思考加工一个竖式纸盒需要几张长方形和正方形纸板？加工一个横式纸盒呢？
请填写下表（设加工x只竖式纸盒，y只横式纸盒，恰好能将购进的纸板全部用完）：
根据上表可得方程组$\left\{\begin{array}{l}{x+2y=1000}\\{4x+3y=2000}\end{array}\right.$；解这个方程组，得$\left\{\begin{array}{l}{x=200}\\{y=400}\end{array}\right.$．
（2）该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板50张，长方形纸板a张，全部加工成上述两种纸盒，且120＜a＜136，试求在这一天加工两种纸盒时，a的所有可能值．
（1）若该厂购进正方形纸板1000张，长方形纸板2000张，问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完．
分析：思考加工一个竖式纸盒需要几张长方形和正方形纸板？加工一个横式纸盒呢？
请填写下表（设加工x只竖式纸盒，y只横式纸盒，恰好能将购进的纸板全部用完）：
| x只竖式纸盒中 | y只横式纸盒中 | 合计 | |
| 正方形纸板的张数 | x | 2y | 1000 |
| 长方形纸板的张数 | 4x | 3y | 2000 |
（2）该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板50张，长方形纸板a张，全部加工成上述两种纸盒，且120＜a＜136，试求在这一天加工两种纸盒时，a的所有可能值．
5．如果a=（-π）0，b=（-0.2）-1，c=（-$\frac{1}{2}$）-2，那么a、b、c三个数的大小为（ ）
| A． | a＞b＞c | B． | c＞a＞b | C． | a＞c＞b | D． | c＞b＞a |
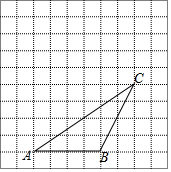如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移2格．