题目内容
13.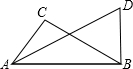 如图,已知∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,试求BC的长.
如图,已知∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,试求BC的长.
分析 首先由直角三角形ABD中,∠BAD=30°,得BD=$\frac{1}{2}$AD=6,则由已知得AC=BD=6,再由勾股定理求出AB,然后由直角三角形ACB运用勾股定理求出BC.
解答 解:∵∠ABD=∠C=90°,AD=12,AC=BD,∠BAD=30°,
∴BD=$\frac{1}{2}$AD=$\frac{1}{2}$×12=6,
∴AC=BD=6,
在直角三角形ABD中,根据勾股定理得:
AB=$\sqrt{A{D}^{2}-B{D}^{2}}$=6$\sqrt{3}$,
在直角三角形ACB中,根据勾股定理得:
BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=6$\sqrt{2}$.
点评 此题考查了勾股定理、含30°角的直角三角形的性质;熟练掌握勾股定理是解决问题的关键.

练习册系列答案
相关题目
15.若△ABC的三边a、b、c满足a2+b2+c2+338=10a+24b+26c,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
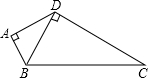 如图,在四边形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,则点D到BC边的距离等于2.
如图,在四边形ABCD中,∠A=90°,∠BDC=90°,AD=2,∠ADB=∠C,则点D到BC边的距离等于2.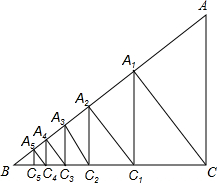 如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C2作C2A2⊥AB,垂足为A2,再过A3作A3C3⊥BC,垂足为C3,…,这样一直做下去,得到了一组线段CA1,A1C1,C2A2,…,则$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.
如图,已知Rt△ABC中,AC=3,BC=4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C2作C2A2⊥AB,垂足为A2,再过A3作A3C3⊥BC,垂足为C3,…,这样一直做下去,得到了一组线段CA1,A1C1,C2A2,…,则$\frac{{C}_{n-1}{A}_{n}}{{A}_{n}{C}_{n}}$=$\frac{5}{4}$.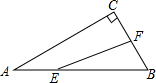 如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC的中点.若动点E以2cm/s的速度从A点出发,沿着A→B→A的方向运动,设运动时间为t(s)(0≤t≤3),连接EF,当t为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s时,△BEF是直角三角形.
如图,在△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,F是BC的中点.若动点E以2cm/s的速度从A点出发,沿着A→B→A的方向运动,设运动时间为t(s)(0≤t≤3),连接EF,当t为1s或3s或$\frac{7}{4}$s或$\frac{9}{4}$s时,△BEF是直角三角形.