题目内容
20.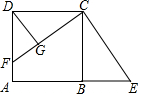 如图,正方形ABCD中,AB=20,F为AD上的点,连接CF,作CE⊥CF交AB的延长线于点E,作DG⊥CF于点G,若BE=15,CE=25,则DG的长度为12.
如图,正方形ABCD中,AB=20,F为AD上的点,连接CF,作CE⊥CF交AB的延长线于点E,作DG⊥CF于点G,若BE=15,CE=25,则DG的长度为12.
分析 根据正方形性质得:∠ADC=∠CBE,CD=BC,证明△FDC≌△EBC,得DF=BE=15,FC=EC=25,由勾股定理求DC的长,再根据面积法求DG的长.
解答 解:∵四边形ABCD为正方形,
∴∠ADC=∠ABC=∠DCB=90°,CD=BC,
∴∠ADC=∠CBE=90°,∠DCF+∠BCF=90°,
∵EC⊥CF,
∴∠ECF=90°,
∴∠BCF+∠BCE=90°,
∴∠DCF=∠BCE,
∴△FDC≌△EBC,
∴DF=BE=15,FC=EC=25,
由勾股定理得:DC=$\sqrt{F{C}^{2}-D{F}^{2}}$=$\sqrt{2{5}^{2}-1{5}^{2}}$=20,
∵DG⊥FC,
∴S△DCF=$\frac{1}{2}$DF•DC=$\frac{1}{2}$FC•DG,
15×20=25DG,
DG=12.
故答案为:12.
点评 本题考查了正方形、全等三角形的性质和判定,在正方形中,常利用同角的余角相等来证明角相等,为三角形全等创造条件,本题还利用了面积法求线段的长,这在几何证明中经常运用,要熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在平面直角坐标中,将直线l1:y=2x平移后,得到直线l1:y=2x+6,则下列平移说法正确的是( )
| A. | 将l1向上平移6个单位长度 | B. | 将l1向下平移6个单位长度 | ||
| C. | 将l1向左平移6个单位长度 | D. | 将l1向右平移6个单位长度 |
8. 如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )
如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )
 如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )
如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )| A. | $\overrightarrow{AD}$=$\overrightarrow{EB}$ | B. | $\overrightarrow{AB}$=$\overrightarrow{DC}$ | C. | $\overrightarrow{AB}$=$\overrightarrow{DE}$ | D. | $\overrightarrow{AD}$=$\overrightarrow{EC}$ |
5.下列结论正确的是( )
| A. | 度数相等的弧相等 | B. | 三点确定一个圆 | ||
| C. | 圆是轴对称图形 | D. | 平分弦的直径垂直于弦 |
 如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC.
如图,在∠MON的两边上取A,B两点,连AB,分别以OA,AB为边,在∠MON内作等边△OAD和等边△ABC,连CD,求证:OB=DC. 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13.若P(m,2)在第13段抛物线C13上,则m的值为37或38.
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C13.若P(m,2)在第13段抛物线C13上,则m的值为37或38. 如图,若在象棋棋盘上建立直角坐标系,使“兵”位于点(-5,1),“炮”位于点(-2.0),则“帥”位于的点的坐标为(-3,-2).
如图,若在象棋棋盘上建立直角坐标系,使“兵”位于点(-5,1),“炮”位于点(-2.0),则“帥”位于的点的坐标为(-3,-2).