题目内容
5.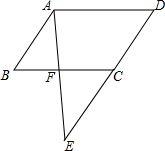 已知四边形ABCD为平行四边形,F在BC上,E在DC的延长线上,且AF:EF=2:3.求:
已知四边形ABCD为平行四边形,F在BC上,E在DC的延长线上,且AF:EF=2:3.求:(1)CF:BF;
(2)BF:AD;
(3)CE:ED.
分析 (1)由四边形ABCD为平行四边形,得到AB∥CD,AD∥BC,推出AB∥CE,根据平行线分线段成比例得到$\frac{CF}{BF}=\frac{EF}{AF}$,代入已知条件即可得到结论;
(2)由CF:BF=3:2,推出BF:BC=2:5,等量代换得到结果;
(3)由BC∥AD,推出CF∥AD,由于AF:EF=2:3,得到EF:AE=3:5,于是得到结论.
解答 解:(1)∵四边形ABCD为平行四边形,
∴AB∥CD,AD∥BC,
∴AB∥CE,
∴$\frac{CF}{BF}=\frac{EF}{AF}$,
∵AF:EF=2:3,
∴CF:BF=3:2;
(2)∵CF:BF=3:2,
∴BF:BC=2:5,
∵AD=BC,
∴BF:AD=2:5;
(3)∵BC∥AD,
∴CF∥AD,
∵AF:EF=2:3,
∴EF:AE=3:5,
∴CE:ED=EF:AE=3:5.
点评 本题考查了平行线分线段成比例,平行四边形性质,熟练掌握各定理是解题的关键.

练习册系列答案
相关题目
16.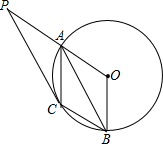 如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点.
如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点.
(1)求证:四边形OACB是菱形;
(2)延长OA至P使得0A=AP,连接PC,求证:PC是⊙O的切线.
 如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点.
如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点. (1)求证:四边形OACB是菱形;
(2)延长OA至P使得0A=AP,连接PC,求证:PC是⊙O的切线.
 如图,已知抛物线y=-x2+2x+1交x轴于A、B点,交y轴于C点,直线l过点C,D(-1,0)两点且交抛物线于P点,求四边形ABPC的面积.
如图,已知抛物线y=-x2+2x+1交x轴于A、B点,交y轴于C点,直线l过点C,D(-1,0)两点且交抛物线于P点,求四边形ABPC的面积. 如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2015m停下,则这个微型机器人停在( )
如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2015m停下,则这个微型机器人停在( )