题目内容
5.(1)如图1,在Rt△ABC中,∠ABC=90°,以点B为中心,把△ABC逆时针旋转90°,得到△A1BC1;再以点C为中心,把△ABC顺时针旋转90°,得到△A2B1C,连接C1B1,则C1B1与BC的位置关系为平行;(2)如图2,当△ABC是锐角三角形,∠ABC=α(α≠60°)时,将△ABC按照(1)中的方式旋转α,连接C1B1,探究C1B1与BC的位置关系,写出你的探究结论,并加以证明;
(3)如图3,在图2的基础上,连接B1B,若C1B1=$\frac{2}{5}$BC,△C1BB1的面积为4,则△B1BC的面积为10.
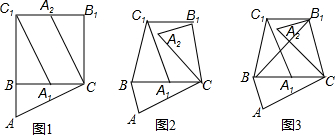
分析 (1)根据旋转变换的性质、平行四边形的判定定理得到四边形A1CA2C1是平行四边形,根据平行四边形的性质证明;
(2)过C1作C1E∥B1C,交BC于E,证明四边形C1ECB1是平行四边形即可;
(3)根据两平行线间的距离相等求出△C1BB1的面积与△B1BC的面积之比,计算即可.
解答 解:(1)由旋转的性质可知,∠ACA2=90°,A1C1=A2C,∠BA1C1=∠A,
∴∠ACB+∠BCA2=90°,
∴∠BA1C1=∠BCA2,
∴A1C1∥A2C,又A1C1=A2C,
∴四边形A1CA2C1是平行四边形,
∴C1B1∥BC,
故答案为:平行;
(2)C1B1∥BC;
证明:过C1作C1E∥B1C,交BC于E,则∠C1EB=∠B1CB,
由旋转的性质知,BC1=BC=B1C,∠C1BC=∠B1CB,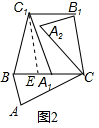
∴∠C1BC=∠C1EB,
∴C1B=C1E,
∴C1E=B1C,
∴四边形C1ECB1是平行四边形,
∴C1B1∥BC;
(3)∵C1B1=$\frac{2}{5}$BC,
∴$\frac{{C}_{1}{B}_{1}}{CB}$=$\frac{2}{5}$,
由(2)得,C1B1∥BC,
∴△C1BB1的面积:△B1BC的面积=$\frac{{C}_{1}{B}_{1}}{CB}$=$\frac{2}{5}$,
∵△C1BB1的面积为4,
∴△B1BC的面积为10,
故答案为:10.
点评 本题考查的是旋转变换的性质、三角形的性质、平行四边形的判定和性质,掌握两平行线间的距离相等、旋转变换的性质是解题的关键.

练习册系列答案
相关题目
15.下列长度的三条线段能组成三角形的是( )
| A. | 2,3,4 | B. | 3,3,6 | C. | 1,2,3 | D. | 5,10,4 |
16.若分式$\frac{3x-6}{2x+1}$的值为0,则x的值为( )
| A. | 2 | B. | 3 | C. | $-\frac{1}{2}$ | D. | $-\frac{1}{2}$或2 |
17.对于函数y=-2x+4.下列说法错误的是( )
| A. | y随x的增大而减小 | B. | 它的图象与y轴的交点是(0,4) | ||
| C. | 当x<2时,y<0 | D. | 它的图象不经过第三象限 |
 如图,已知∠ABD=40°,∠ACD=35°,∠A=55°,则∠BDC=130°.
如图,已知∠ABD=40°,∠ACD=35°,∠A=55°,则∠BDC=130°.