题目内容
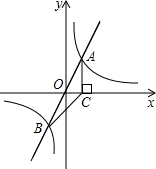 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=| k |
| x |
(1)求反比例函数的解析式;
(2)若点P是反比例函数y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A点横坐标代入正比例函数可求得A点坐标,代入反比例函数解析式可求得k,可求得反比例函数解析式;
(2)由条件可求得B、C的坐标,可先求得△ABC的面积,再结合△OPC与△ABC的面积相等求得P点坐标.
(2)由条件可求得B、C的坐标,可先求得△ABC的面积,再结合△OPC与△ABC的面积相等求得P点坐标.
解答:解:
(1)把x=2代入y=2x中,得y=2×2=4,
∴点A坐标为(2,4),
∵点A在反比例函数y=
的图象上,
∴k=2×4=8,
∴反比例函数的解析式为y=
;
(2)∵AC⊥OC,
∴OC=2,
∵A、B关于原点对称,
∴B点坐标为(-2,-4),
∴B到OC的距离为4,
∴S△ABC=2S△ACO=2×
×2×4=8,
∴S△OPC=8,
设P点坐标为(x,
),则P到OC的距离为|
|,
∴
×|
|×2=8,解得x=1或-1,
∴P点坐标为(1,8)或(-1,-8).
(1)把x=2代入y=2x中,得y=2×2=4,
∴点A坐标为(2,4),
∵点A在反比例函数y=
| k |
| x |
∴k=2×4=8,
∴反比例函数的解析式为y=
| 8 |
| x |
(2)∵AC⊥OC,
∴OC=2,
∵A、B关于原点对称,
∴B点坐标为(-2,-4),
∴B到OC的距离为4,
∴S△ABC=2S△ACO=2×
| 1 |
| 2 |
∴S△OPC=8,
设P点坐标为(x,
| 8 |
| x |
| 8 |
| x |
∴
| 1 |
| 2 |
| 8 |
| x |
∴P点坐标为(1,8)或(-1,-8).
点评:本题主要考查待定系数法求函数解析式及函数的交点问题,在(1)中求得A点坐标、在(2)中求得P点到OC的距离是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知关于x的方程
+2=
有解,则k的取值范围是( )
| 1-x |
| x-2 |
| k |
| 2-x |
| A、k≠1 | B、k≠2 |
| C、k>1 | D、k≠-1 |
已知a,b互为相反数,c、d互为倒数,且|m|=3,则2a-4m2+2b-(cd)2015=( )
| A、-2051 | B、-35 |
| C、-36 | D、-37 |
已知两点的坐标分别是(-2,3)和(2,3),则下列情况:①两点关于x轴对称.②两点关于y轴对称.③两点之间距离为4.其中都正确的有( )
| A、①② | B、①③ | C、②③ | D、①②③ |
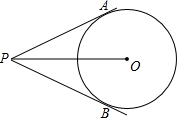 已知PA切⊙O于点A,PB切⊙O于点B,PO=4,PA=2
已知PA切⊙O于点A,PB切⊙O于点B,PO=4,PA=2