题目内容
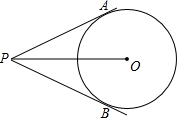 已知PA切⊙O于点A,PB切⊙O于点B,PO=4,PA=2
已知PA切⊙O于点A,PB切⊙O于点B,PO=4,PA=2| 3 |
考点:切线的性质
专题:
分析:连接OA.根据切线的性质知△POA为直角三角形.运用三角函数的定义可求∠OPA;根据切线长定理知∠APB=2∠APO.
解答: 解:如图所示,连接OA.
解:如图所示,连接OA.
∵PA切⊙O于点A,
∴OA⊥PA.
∵cos∠APO=
=
=
,
∴∠APO=30°.
∵PB切⊙O于B,
∴∠APB=2∠APO=60°.
故答案为 60.
 解:如图所示,连接OA.
解:如图所示,连接OA.∵PA切⊙O于点A,
∴OA⊥PA.
∵cos∠APO=
| PA |
| PO |
2
| ||
| 4 |
| ||
| 2 |
∴∠APO=30°.
∵PB切⊙O于B,
∴∠APB=2∠APO=60°.
故答案为 60.
点评:此题考查切线的性质、切线长定理及三角函数定义等知识点,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

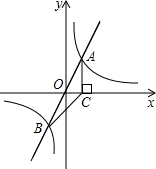 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y= a,b是有理数,它们在数轴上的对应点的位置如图,把a,-a,b,-b按由大到小的顺序排列,并用“>”连接为
a,b是有理数,它们在数轴上的对应点的位置如图,把a,-a,b,-b按由大到小的顺序排列,并用“>”连接为