题目内容
2. 已知直线y=-$\frac{1}{2}$x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以$\sqrt{2}$个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.
已知直线y=-$\frac{1}{2}$x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以$\sqrt{2}$个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.(1)∠BCO=45°°;
(2)求y关于t的函数关系式及自变量t的取值范围;
(3)是否存在时间t,使得以PC为直径的⊙D与直线QM相切?若存在,求t的值;不存在,说明理由.
分析 (1)先分别求得点A和点B的坐标,从而得到点C的坐标,从而得到OB=OC,于是可求得∠BCO的度数;
(2)先由相似三角形的性质得到CM的长,然后依据PM=CO+CM-OP可求得y与t的函数关系式;
(3)当点P在点C的左边时,可求得DM=1,由tan∠NMD=$\frac{1}{2}$,可求得DN=$\frac{\sqrt{5}}{5}$,然后可求得DC=1-t,从而可求得t的值;当点P在点C的右侧时,可求得DC=t-1,DN=$\frac{\sqrt{5}}{5}$,从而可求得t的值.
解答 解:(1)∵令y=0得-$\frac{1}{2}$x+2=0,解得:x=4,
∴A(0,4).
∴OA=4.
∵点C为线段OA的中点,
∴OC=2.
∵令x=0得:y=2,
∴B(0,2).
∴OB=2.
∴OB=OC.
又∵∠BOC=90°,
∴∠BCO=45°.
故答案为:45.
(2)如图1所示: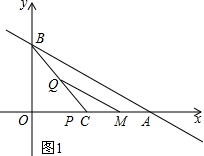
∵OB=CO=2,∠BOC=90°,
∴BC=$\sqrt{2}$OB=2$\sqrt{2}$.
∵OA=4,OC=2,
∴AC=2.
设点P和点Q的运动时间为t,则OP=2t,QP=$\sqrt{2}$t.
∵QM∥AB,
∴$\frac{CQ}{BC}=\frac{CM}{AC}$,即$\frac{\sqrt{2}t}{2\sqrt{2}}=\frac{CM}{2}$,解得CM=t.
∴PM=CO+CM-OP=2+t-2t=2-t(0≤t≤2).
∴y与t的函数关系是为y=2-t(0≤t≤2).
(3)如图2所示:设N为切线,连接DN.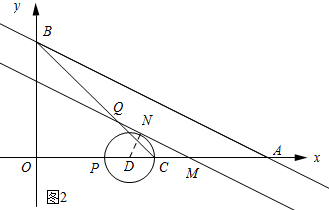
∵OP=2t,OC=2,
∴PC=2-2t.
∴PD=DC=1-t.
∴DM=PM-PD=2-t-(1-t)=1.
∵MQ是圆D的切线,
∴DN⊥QM.
∵OB=2,OA=4,
∴tan∠BAO=$\frac{1}{2}$.
∵QM∥AB,
∴tan∠NMP=$\frac{1}{2}$.
∴DN=$\frac{\sqrt{5}}{5}$DM=$\frac{\sqrt{5}}{5}$.
∴1-t=$\frac{\sqrt{5}}{5}$,解得:t=1$-\frac{\sqrt{5}}{5}$.
如图3所示:设N为切线,连接DN.
∵OP=2t,OC=2,
∴PC=2t-2.
∴DC=DP=t-1.
∴DM=t-1+2-t=1.
∴DN=$\frac{\sqrt{5}}{5}$.
∴t-1=$\frac{\sqrt{5}}{5}$,解得:t=1+$\frac{\sqrt{5}}{5}$.
综上所述,当t=1-$\frac{\sqrt{5}}{5}$或t=1+$\frac{\sqrt{5}}{5}$时,以PC为直径的⊙D与直线QM相切.
点评 本题主要考查的是一次函数的综合应用,解答本题主要应用了一次函数图象上点的坐标与函数解析式的关系、等腰直角三角形的判定、切线的性质、锐角三角函数的定义、相似三角形的性质和判定,求得DM、DN、CD的长是解题的关键.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案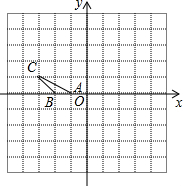 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,0),C(-3,1).将△ABC绕点A按顺时针方向旋转90°,得到
△AB′C′,则点B′的坐标为( )
| A. | (-1,1) | B. | (2,3) | C. | (4,1) | D. | (0,2) |
| A. | a>1 | B. | a≥1 | C. | a<1 | D. | a≤1 |
| A. | 调查市场上某种牛奶中蛋白质的含量 | |
| B. | 调查鞋厂生产的鞋底能承受的弯折次数 | |
| C. | 了解某班学生感染流感病毒的人数 | |
| D. | 了解我市“十三”规划知晓的情况 |
| A. | (9,0) | B. | (-9,0) | C. | (0,-9) | D. | (0,9) |
| A. | 一、二、三 | B. | 一、三、四 | C. | 二、三、四, | D. | 一、二、四 |