题目内容
17.若以正方形ABCD的一边CD为边作等边三角形△CDE,则∠BED=45或135°.分析 解答本题时要考虑两种情况,E点在正方形内和外两种情况,由正方形和等边三角形的性质容易得出结果.
解答 解:分两种情况: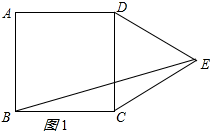
①当点E在正方形ABCD外侧时,如图1所示:
∵四边形ABCD是正方形,△CDE是等边三角形
∴∠BCD=90°,BC=CD=CE,∠DCE=∠CED=60°,
∴∠BCE=90°+60°=150°,
∵BC=CE,
∴∠CEB═∠CBE=15°,
∴∠BED=60°-15°=45°;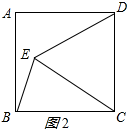
②当点E在正方形ABCD内侧时,如图2所示:
∵∠CED=∠DCE=60°,∠BCD=90°,
∴∠BCE=30°,
∵BC=CE,
∴∠BEC=∠EBC=75°,
∴∠BED=60°+75°=135°;
综上所述:∠BED为45°或135°;
故答案为:45或135.
点评 本题考查了正方形的性质、等边三角形的性质、钝角三角形的性质、三角形内角和定理等知识;熟练掌握正方形和等边三角形的性质,通过进行分类讨论得出结果是解题的关键

练习册系列答案
相关题目
7.若代数式a2-2ab=7,那么代数式3ab-$\frac{3}{2}$a2-2的值是( )
| A. | $\frac{17}{2}$ | B. | 5 | C. | -$\frac{17}{2}$ | D. | -$\frac{25}{2}$ |
8. 如图:一次函数y=kx+b的图象经过A、B两点,则不等式kx+b>0的解集是( )
如图:一次函数y=kx+b的图象经过A、B两点,则不等式kx+b>0的解集是( )
 如图:一次函数y=kx+b的图象经过A、B两点,则不等式kx+b>0的解集是( )
如图:一次函数y=kx+b的图象经过A、B两点,则不等式kx+b>0的解集是( )| A. | x>0 | B. | x>2 | C. | x>-3 | D. | -3<x<2 |
5.下列计算正确的是( )
| A. | (ab3)2=a2b6 | B. | a2•a3=a6 | C. | (a+b)(a-2b)=a2-2b2 | D. | 5a-2a=3 |
12.下列说法正确的是( )
| A. | 对角线互相垂直的四边形是平行四边形 | |
| B. | 对角线相等且互相平分的四边形是矩形 | |
| C. | 对角线相等且互相垂直的四边形是菱形 | |
| D. | 对角线互相垂直的平行四边形是正方形 |
9.下列各组长度的3条线段,不能构成三角形的是( )
| A. | 6cm、5cm、10cm | B. | 5cm、4cm、9cm | C. | 4cm、6cm、9cm | D. | 2cm、3cm、4cm |
6.下列各组数不能组成直角三角形的是( )
| A. | a=7,b=24,c=25 | B. | a=11,b=60,c=61 | C. | a=$\frac{8}{3}$,b=2,c=$\frac{13}{3}$ | D. | a=1,b=$\frac{5}{4}$,c=$\frac{3}{4}$ |
 已知直线y=-$\frac{1}{2}$x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以$\sqrt{2}$个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度.
已知直线y=-$\frac{1}{2}$x+2分别交x、y轴于点A、B,点C为线段OA的中点,动点P从坐标原点出发,以2个单位长度/秒的速度向终点A运动,动点Q从点C出发,以$\sqrt{2}$个单位长度/秒的速度向终点B运动.过点Q作QM∥AB交x轴于点M,动点P、Q同时出发,其中一个点到达终点,另一个点也停止运动,设点P运动的时间为t秒,PM的长为y个单位长度. 如图,在菱形ABCD中,对角线AC=10,BD=24,
如图,在菱形ABCD中,对角线AC=10,BD=24,