题目内容
13. 如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.
如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.(1)求证:BC为⊙O的切线.
(2)若sinA=$\frac{3}{5}$,BC=6,求⊙O的半径.
分析 (1)根据在同圆或等圆中,同弧所对的圆周角相等可得∠A=∠E,再根据三角形的内角和等于180°求出∠ABC=90°,然后根据切线的定义证明即可;
(2)根据∠A的正弦求出AC,利用勾股定理列式计算求出AB,然后求解即可.
解答 (1)证明:∵∠A与∠E所对的弧都是$\widehat{BD}$,
∴∠A=∠E,
又∵∠E+∠C=90°,
∴∠A+∠C=90°,
在△ABC中,∠ABC=180°-90°=90°,
∵AB为直径,
∴BC为⊙O的切线;
(2)解:∵sinA=$\frac{3}{5}$,BC=6,
∴$\frac{BC}{AC}$=$\frac{3}{5}$,
即$\frac{6}{AC}$=$\frac{3}{5}$,
解得AC=10,
由勾股定理得,AB=$\sqrt{A{C}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵AB为直径,
∴⊙O的半径是$\frac{1}{2}$×8=4.
点评 本题考查了切线的判定,锐角三角函数,解直角三角形,勾股定理,在同圆或等圆中,同弧所对的圆周角相等的性质,熟记切线的概念并求出直角是解题的关键.

练习册系列答案
相关题目
8.一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利情况如表所示:
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
| 销售方式 | 粗加工后销售 | 精加工后销售 |
| 每吨获利(元) | 1000 | 2000 |
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
5.在直角坐标中,点P(2,-3)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.如果$\sqrt{\frac{x}{x-3}}=\frac{\sqrt{x}}{\sqrt{x-3}}$成立,那么( )
| A. | x≥3 | B. | 0≤x≤3 | C. | x≥0 | D. | x>3 |
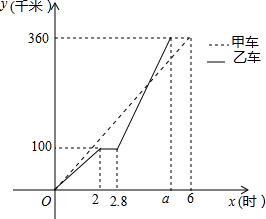 甲、乙两车同时从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍,两车行驶路程y(千米)与行驶时间x(时)的函数图象如图所示,
甲、乙两车同时从A地前往B地,乙行驶途中有一次停车修理,修好后乙车的行驶速度是原来的2倍,两车行驶路程y(千米)与行驶时间x(时)的函数图象如图所示,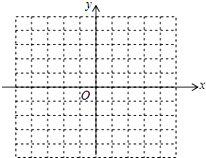 在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出将△ABC向右平移3个单位得到的△A1B1C1.
在平面直角坐标系中,已知点A(-3,1),B(-1,0),C(-2,-1),请在图中画出△ABC,并画出将△ABC向右平移3个单位得到的△A1B1C1.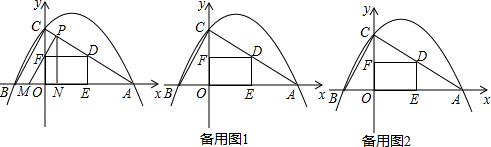
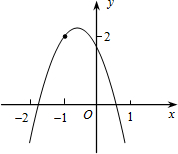 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1,下列结论:
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标分别为x1、x2,其中-2<x1<-1,0<x2<1,下列结论: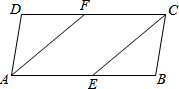 如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,
如图,在平行四边形ABCD中,已知AF平分∠DAB,CE平分∠BCD,