题目内容
16.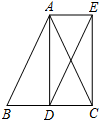 如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A、D作AE∥BC、DE∥AB,AE与DE相交于点E,连结CE.求证:四边形ADCE是矩形.
如图,在△ABC中,AB=AC,AD平分∠BAC交BC于点D,分别过点A、D作AE∥BC、DE∥AB,AE与DE相交于点E,连结CE.求证:四边形ADCE是矩形.
分析 先证明四边形ABDE是平行四边形,得出AE=BD,由等腰三角形的性质得出BD=CD,AD⊥BC,得出AE=CD,∠ADC=90°,证出四边形ADCE是平行四边形.即可得出结论.
解答 证明∵AE∥BC、DE∥AB,
∴四边形ABDE是平行四边形.
∴AE=BD,
∵AB=AC,AD平分∠BAC,
∴BD=CD,AD⊥BC,
∴AE=CD,∠ADC=90°,
又∵AE∥BC,
∴四边形ADCE是平行四边形.
∴四边形ADCE是矩形.
点评 本题考查了平行四边形的判定与性质、矩形的判定、等腰三角形的性质;熟练掌握平行四边形的判定与性质,由等腰三角形的性质得出BD=CD,AD⊥BC是解决问题的关键.

练习册系列答案
相关题目
6.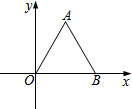 如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
 如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )
如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=4,则点A的坐标为( )| A. | (2,$\sqrt{3}$) | B. | (2,4) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{3}$,2) |
11.一个不透明的盒子中装有6个大小相同的乒乓球,其中4个是黄球,2个是白球.从该盒子中任意摸出一个球,摸到黄球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{5}$ |
8. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线.点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第15秒时,点P的坐标是( )
如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线.点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第15秒时,点P的坐标是( )
 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线.点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第15秒时,点P的坐标是( )
如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,…组成一条平滑的曲线.点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第15秒时,点P的坐标是( )| A. | (15,1) | B. | (15,-1) | C. | (30,1) | D. | (30,-1) |
3.若整数x能使分式$\frac{3x-3}{{x}^{2}-1}$的值是整数,则符合条件的x的值有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
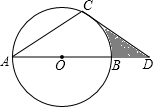 如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.
如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠D=30°.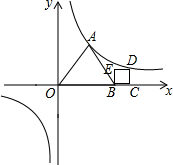 已知,反比例函数y=$\frac{\sqrt{3}}{x}$的图象上有两点A和D,且△OBA是等边三角形,四边形BCDE是正方形,则D点坐标(1+$\sqrt{\sqrt{3}+1}$,-1+$\sqrt{\sqrt{3}+1}$).
已知,反比例函数y=$\frac{\sqrt{3}}{x}$的图象上有两点A和D,且△OBA是等边三角形,四边形BCDE是正方形,则D点坐标(1+$\sqrt{\sqrt{3}+1}$,-1+$\sqrt{\sqrt{3}+1}$).