题目内容
7.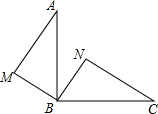 在△AMB中,∠AMB=90°,将△AMB以B为中心顺时针旋转90°,得到△CNB.
在△AMB中,∠AMB=90°,将△AMB以B为中心顺时针旋转90°,得到△CNB.求证:AM∥NB.
分析 由旋转的性质得出△AMB≌△CNB,∠ABC=90°,得出∠ABM=∠CBN,∠ABN+∠CBN=90°,证出∠MBN=90°,得出∠AMB+∠MBN=180°,即可得出结论.
解答 证明:由旋转的性质得:△AMB≌△CNB,∠ABC=90°,
∴∠ABM=∠CBN,∠ABN+∠CBN=90°,
∴∠ABM+∠ABN=90°,
即∠MBN=90°,
∴∠AMB+∠MBN=90°+90°=180°,
∴AM∥NB.
点评 本题考查了平行线的判定、旋转的性质、全等三角形的性质;熟练掌握旋转的性质,证明∠MBN=90°是解决问题的关键.

练习册系列答案
相关题目
12.若x,y为实数,且$\sqrt{2x+y}$+(x-y+3)2=0,则x+y的值为( )
| A. | 0 | B. | -1 | C. | 1 | D. | 5 |
19.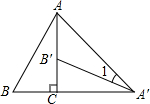 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( )
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=27°,则∠B的度数是( )| A. | 84° | B. | 72° | C. | 63° | D. | 54° |
17.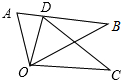 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数为( )
如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数为( )
 如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数为( )
如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠DOB的度数为( )| A. | 36° | B. | 38° | C. | 34° | D. | 40° |