题目内容
古希腊著名的毕达哥拉斯学派把1、3、6、10 …这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.
(1)49是一个正方形数,请你把它写成两个三角形数和的形式49= + ;
(2)如果用∑n表示从1开始到n的连续整数的和,(即:∑n=1+2+3+4+…+n),那么:∑n+∑n+1= ;
(3)试用图形来说明:∑n=
.
(1)49是一个正方形数,请你把它写成两个三角形数和的形式49=
(2)如果用∑n表示从1开始到n的连续整数的和,(即:∑n=1+2+3+4+…+n),那么:∑n+∑n+1=
(3)试用图形来说明:∑n=
| (n+1)2-(n+1) |
| 2 |
考点:规律型:数字的变化类,规律型:图形的变化类
专题:
分析:(1)用点排列的正方形数,以对角线为分界线,对角线以上的为一个三角形数,对角线以下包括对角线是另一个三角形数,因为1+2+3+4+5+6=21,1+2+3+4+5+6+7=28,且49=21+28,由此得出答案即可;
(2)利用求和的定义得出答案即可;
(3)看作正方形数(n+1)2为三角形数和∑n+∑n+1再减去三角形数∑n+1和的一半,由此画出图形即可.
(2)利用求和的定义得出答案即可;
(3)看作正方形数(n+1)2为三角形数和∑n+∑n+1再减去三角形数∑n+1和的一半,由此画出图形即可.
解答:解:(1)49=21+28;
(2)∑n+∑n+1=
n(n+1)+
(n+1)(n+1+1)=(n+1)2;
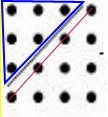
(3)∑n=
(n+1)2-
(n+1),
如图:


(2)∑n+∑n+1=
| 1 |
| 2 |
| 1 |
| 2 |
(3)∑n=
| 1 |
| 2 |
| 1 |
| 2 |
如图:



点评:本题考查了整式的混合运算及规律型:数字的变化类,首先要观察出“三角形数”和“正方形数”的变化规律,再根据规律解题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )
如图,三角形纸片ABC,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为( )| A、9cm | B、13cm |
| C、16cm | D、10cm |
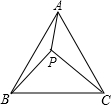 如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.
如图,已知点P是等边△ABC内一点,PA=3,PB=4,PC=5,求∠APB的度数.