题目内容
填空：如图，已知∠EFD=∠BCA，BC=EF，AF=DC，则AB=DE，请说明理由．解：因为AF=DC（已知）
所以AF+
即
在△ABC和△DEF中
BC=EF（已知）
所以△ABC≌△DEF（
则AB=DE．
考点：全等三角形的判定与性质
专题：推理填空题
分析：先根据等式的性质得AC=FD，再根据SAS证明△ABC≌△DEF，利用全等三角形对应边相等得AB=DE．
解答：解：因为AF=DC（已知）
所以AF+FC=DC+FC，
即 AC=DF，
在△ABC和△DEF中，
，
∴△ABC≌△DEF（SAS）
则AB=DE．
故答案为：FC，FC，AC=DF，∠EFD=∠BCA，AC=DF，SAS．
所以AF+FC=DC+FC，
即 AC=DF，
在△ABC和△DEF中，
|
∴△ABC≌△DEF（SAS）
则AB=DE．
故答案为：FC，FC，AC=DF，∠EFD=∠BCA，AC=DF，SAS．
点评：本题考查三角形全等的判定方法及性质，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
练习册系列答案
相关题目
如图，在6×6的方格纸中，每个小方格都是边长为1的正方形，其中A、B、C为格点，作△ABC的外接圆⊙O，则弧AC的长等于计算：-x2•（-x）2等于（ ）
| A、（-x）2+2=（-x）4=x4 |
| B、-x2•（-x）2=-x2+2=-x4 |
| C、-x2•x2=-x2+2=-x4 |
| D、-x2•x2=-x2×2=-x4 |
已知：如图，AB∥CD，AB=CD，点B、E、F、D在同一直线上，∠A=∠C．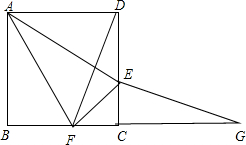
在正方形ABCD中，E、F分别是边CD、BC上的点，且CE=CF，点G是BC延长线上的一点且∠CEG+∠CDF=90°，连结EF、AE、AF．
如图，AB是⊙O的切线，切点为B，AO交⊙O于点C，过点C作DC⊥OA交AB于点D
如图，DC是⊙O直径，弦AB⊥CD于点F，连接BC、BD，则下列结论错误的是（ ）| A、AF=BF | ||||
| B、OF=CF | ||||
C、
| ||||
| D、∠DBC=90° |
