题目内容
5. 已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=16,BC=18.连接BD,AE⊥BD,垂足为点E.
已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=16,BC=18.连接BD,AE⊥BD,垂足为点E.(1)求证:△ABE∽△DBC;
(2)求线段BE的长.
分析 (1)由等腰三角形的性质可知∠ABD=∠ADB,由AD∥BC可知,∠ADB=∠DBC,由此可得∠ABD=∠DBC,即可得出结论;
(2)由等腰三角形的性质可知,BD=2BE,根据△ABE∽△DBC,利用相似比求BE即可.
解答 (1)证明:∵AB=AD=16,
∴∠ABD=∠ADB,
∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵AE⊥BD,
∴∠AEB=∠C=90°,
∴△ABE∽△DBC;
(2)解:∵AB=AD,又AE⊥BD,
∴BE=DE,
∴BD=2BE,
由△ABE∽△DBC,
得$\frac{AB}{BD}=\frac{BE}{BC}$,
∵AB=AD=16,BC=18,
∴$\frac{16}{2BE}=\frac{BE}{18}$,
解得:BE=12.
点评 本题考查了相似三角形的判定与性质、等腰三角形的性质;证明三角形相似是解决问题的关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
16.下列各式去括号正确的是( )
| A. | -(2a-b+c)=-2a-b+c | B. | -(x-y)+(xy-1)=-x+y+xy-1 | ||
| C. | -(3b-2c)=-3b-2c | D. | -[x-(5z+4)]=-x-5z+4 |
 如图,在平面直角坐标系中,矩形ABCD的顶点A与坐标原点O重合,B(4,0),D(0,3),点E从点A出发,沿射线AB移动,以CE为直径作⊙M,点F为⊙M与射线DB的公共点,连接EF、CF,过点E作EG⊥EF,EG与⊙M相交于点G,连接CG.
如图,在平面直角坐标系中,矩形ABCD的顶点A与坐标原点O重合,B(4,0),D(0,3),点E从点A出发,沿射线AB移动,以CE为直径作⊙M,点F为⊙M与射线DB的公共点,连接EF、CF,过点E作EG⊥EF,EG与⊙M相交于点G,连接CG. 已知:如图所示,直线l的解析式为y=$\frac{3}{4}$x-3,并且与x轴、y轴分别交于点A、B.
已知:如图所示,直线l的解析式为y=$\frac{3}{4}$x-3,并且与x轴、y轴分别交于点A、B.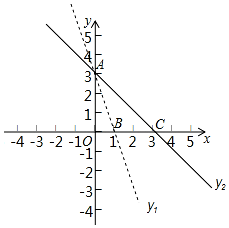 已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3).与x轴的交点坐标为B(1,0)、C(3,0).
已知函数y1=k1x+b1和y2=k2x+b2图象如图所示,直线y1与直线y2交于A点(0,3).与x轴的交点坐标为B(1,0)、C(3,0).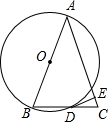 如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.
如图,△ABC的边AB为⊙O的直径,BC与⊙O交于点D,D为BC的中点,过点D作DE⊥AC于E.