题目内容
10. 已知:如图所示,直线l的解析式为y=$\frac{3}{4}$x-3,并且与x轴、y轴分别交于点A、B.
已知:如图所示,直线l的解析式为y=$\frac{3}{4}$x-3,并且与x轴、y轴分别交于点A、B.(1)求A、B两点的坐标;
(2)半径为1的⊙P,从原点以4个单位/秒的速度沿x轴正方向运动,问经过几秒后,点A在⊙P上.
(3)在题(2)中,如果在⊙P开始运动的同时,⊙P的半径以6个单位/秒的速度扩大,⊙P可以经过B点吗?如果能请求出时间;如果不能请说明理由.
分析 (1)对于直线y=$\frac{3}{4}$x-3,令x=0,得y=-3,令y=0得,x=4,可得A、B两点坐标.
(2)设经过ts后点A在⊙P上,根据PA=1列出方程即可解决问题,注意两解.
(3))⊙P可以经过B点,理由如下:设t秒后点B在⊙P上,t秒后点P坐标(4t,0),⊙P的半径为1+6t,由题意,PB2=OB2+OP2,可得方程32+(4t)2=(1+6t)2,解方程即可.
解答 解:(1)对于直线y=$\frac{3}{4}$x-3,令x=0,得y=-3,令y=0得,x=4,
∴A(4,0),B(0,-3).
(2)设经过ts后点A在⊙P上,
∵⊙P的半径为1,
∴PA=1时,点A在⊙P上,
∴P(3,0)或(5,0),
∴4-4t=1或4t-4=1时点A在⊙P上
∴t=$\frac{3}{4}$s或$\frac{5}{4}$s时,点A在⊙P上.
(3)⊙P可以经过B点,理由如下:
设t秒后点B在⊙P上,∵t秒后点P坐标(4t,0),⊙P的半径为1+6t,
由题意,PB2=OB2+OP2,
∴32+(4t)2=(1+6t)2,
整理得5t2+3t-2=0,解得t=$\frac{2}{5}$或-1(舍弃),
∴t=$\frac{2}{5}$时,⊙P经过点B.
点评 本题考查圆综合题,点与圆位置关系,一元一次方程等知识,解题的关键是灵活运用所学知识解决问题,学会用方程的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
 已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=16,BC=18.连接BD,AE⊥BD,垂足为点E.
已知:如图,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=16,BC=18.连接BD,AE⊥BD,垂足为点E.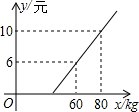 某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图.
某地长途汽车客运公司规定每位旅客可随身携带一定的行李,如果超出规定,那么需要购买行李票,行李票 y(元)是行李质量 x(kg)的一次函数,其图象如图. 已知有理数a、b、c在数轴上的位置如图所示,化简|a+c|-|b-c|.
已知有理数a、b、c在数轴上的位置如图所示,化简|a+c|-|b-c|.