题目内容
18. 如图,已知线段AB长为10cm,C是线段AB上任意一点,则AC的中点与BC的中点之间的距离是( )
如图,已知线段AB长为10cm,C是线段AB上任意一点,则AC的中点与BC的中点之间的距离是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 不能确定 |
分析 根据线段中点的性质,可得MC,NC的长,再根据线段的和差,可得答案.
解答 解:如图: ,
,
M是AC的中点,N是BC的中点,
MC=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC.
由线段的和差,得
MN=MC+NC=$\frac{1}{2}$AC+$\frac{1}{2}$BC
=$\frac{1}{2}$(AC+BC)
=$\frac{1}{2}$AB
=5cm.
故选:C.
点评 本题考查了两点间的距离,利用线段中点的性质得出MC、NC的长是解题关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
13. 如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )
如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )
 如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )
如图,下列式子不能说明点C是线段AB(AC>BC)的黄金分割点的是( )| A. | $\frac{BC}{AC}$=$\frac{\sqrt{5}-1}{2}$ | B. | AC+BC=$\frac{\sqrt{5}-1}{2}$AB | C. | $\frac{AC}{AB}$=$\frac{\sqrt{5}-1}{2}$ | D. | AC2=AB•BC |
10.图中是正方体的平面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
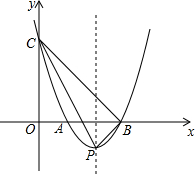 如图所示,已知抛物线与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),P是抛物线的顶点,连接BC,CP,BP.求:
如图所示,已知抛物线与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),P是抛物线的顶点,连接BC,CP,BP.求: 如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的顶点都在格点上,点C的坐标为(0,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的顶点都在格点上,点C的坐标为(0,-1).